My Time in Space (16 page)
Authors: Tim Robinson

In its origins, then, projective geometry relates to the theory
of perspective and to the Enlightenment’s fascination with the new tools of vision, the telescope, the microscope, the camera obscura, and so to the ocular imagery pervading the thought of that time, including Descartes’ foundational doctrine of ‘clear and distinct ideas’ and even his conception of the relationship of soul to body. Later in his life Pascal composed an emblematic ‘device’ for himself, showing an eye surrounded by a crown of thorns. In the daytime world of fact and history, this commemorated ‘the Miracle of the Thorn’, an important event in the turbulent history of Port Royale, the Jansenist abbey with which his family was closely connected: a precious relic, a fragment of a spine from Christ’s crown of thorns, had been lent to the abbey, and Pascal’s niece had been cured of a dreadful fistula or ulcer of a tear-gland by application of the reliquary containing it; the occurrence was investigated by doctors of the Sorbonne and officially declared miraculous. But one could point to other connections, not
figuring
in the Cartesian realm of clear and distinct ideas, between this discomforting image of the eye surrounded by thorns, and that of the eye at the vertex of a cone, at the origin of the generators of form in general and of the mystic hexagram in particular.
The standard proofs of Pascal’s theorem in today’s textbooks use analytic or projective techniques that were not available in his time, or that seem foreign to his ocular and intuitive methods. However there is one proof, discovered in 1826, that uses only the simplest and clearest consequences of a few basic and strikingly visual ideas. Its inventor was Germinal Dandelin, a military
engineer
in Napoleonic France, and later professor of mining
engineering
in Brussels. Hardy, in trying to locate the aesthetic qualities of a proof, as apart from the ‘seriousness’ of the result, writes:
… there is a high degree of unexpectedness, combined with
inevitability
and economy. The arguments take so odd and surprising a form; the weapons used seem so childishly simple when compared with the
far-reaching
results; but there is no escape from the conclusions. There are no complications of detail – one line of attack is enough….
Dandelin’s proof has all these narrative strengths. It is very
dramatic
; it sets off in an apparently irrelevant direction, appears momentarily to be lost in a thicket of lines, and suddenly
confronts
one with the result. I will expound it here, not for its own sake but, if I can, to convey the experience of understanding a proof, the rush of aesthetic adrenaline at its success. (To be
realistic
, perhaps that thrill will only be vouchsafed to those readers who have already trod similar ways, or are prepared to force their way through the thicket several times, to and fro, beating a path in which they will not be snagged by details. As for the others, I would rather they turn the page than abandon me completely!)
We will introduce a few preliminary ideas. (I note that
mathematicians
, including Pascal, frequently use this ‘we’, not because they count themselves kings of infinite space but that they are counting on, imploring, the reader to join with them in the
venture
, to share in the process of proof, which is nothing if it is not followed, and not in blind faith but with a critical mind ready to disconfirm or confirm it. A proof is a rational seduction. Also I should admit that I will glide over some little complications in the following, concerning lines that might be parallel rather than
intersect
; but anyone who has enough geometry to notice these elisions will also be able to fill them in. So, I beg you, follow me and if there are difficulties, jump over them without letting them perturb you.)
In Pascal’s definition of a cone we have already met the
concept
of a line that sweeps out a surface. Dandelin’s proof uses
another form generated by lines, called a hyperboloid of one sheet. Imagine a sphere that can spin on a vertical axis; let a line be fixed to it, touching it at one point on its equator; then if the line is also vertical it will sweep out a cylinder when the sphere is rotated (Fig. 11). But if the line is askew it will sweep out the shape we need (Fig. 12). We will call its successive positions the generators; they are straight lines lying in this curved surface. (It is a common shape for lampshades because it can be made out of strings, playing the role of generators, stretched slantwise between two round loops of wire.) An equally askew line leaning in the other direction would sweep out the same surface, so there are two families of generators. No two generators of the same family intersect, but each generator of one family intersects all those of the other family.
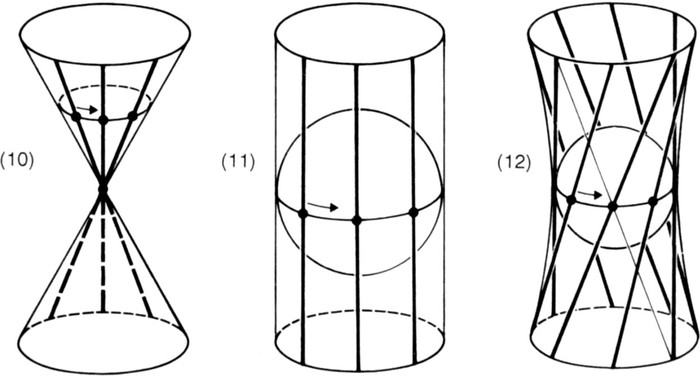
Figs. 10–12. Curved surfaces generated by movement of a line. A few
generators
are shown in each case. (10) the cone; (11) the cylinder; (12) the
hyperboloid
of one sheet, with some generators of the first family shown as bold lines and one generator of the second family as a fine line. (If the generators were extended far enough, the one from the second family would eventually
intersect
with all those from the first family, with the exception of the one directly opposite it, to which it is parallel.)
Having introduced the hyperboloid and its generators all we need are some obvious facts about lines and planes, such as that two intersecting lines define just one plane in which they lie, that two planes intersect in a line, and three planes in a point; for instance, the ceiling and two walls meet at the corner of a room.
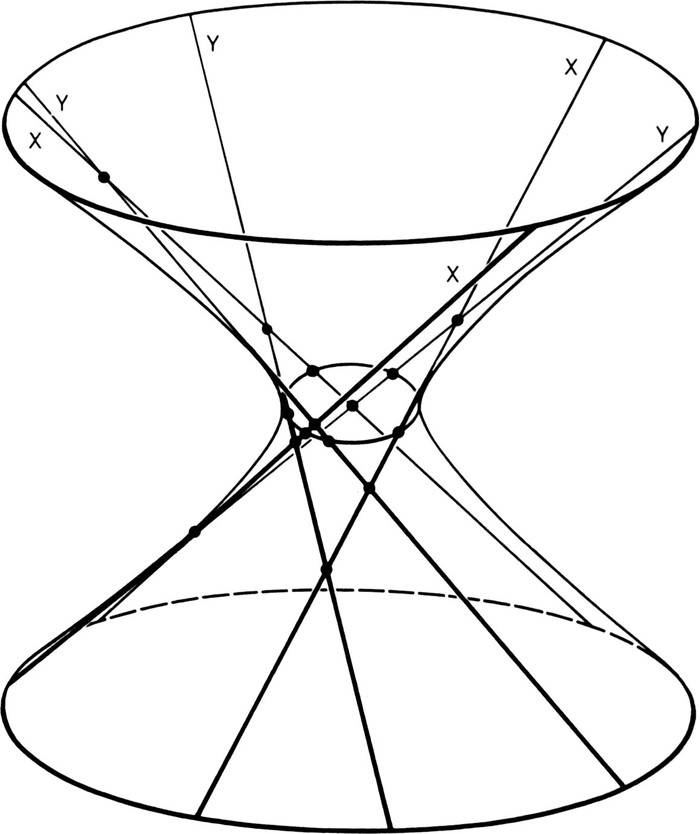
Fig. 13. The hyperboloid, the conic, and the six generators. (For convenience I have drawn the conic in the neck of the hyperboloid, but it could be in any position. Generators are shown by finer lines where they lie on the farther side of the hyperboloid. Generators of one family are marked X and those of the other family Y.)
Now we will take a plane cutting through the hyperboloid; if the plane is horizontal the intersection will be a circle, and if
slanting
, one of the other conic sections (this is easily proved, but we shall take it as established). In the conic we will inscribe a
hexagon
. Through one of its corners we draw a generator belonging to one of the families, through the next corner a generator from the other family, and so on all the way round (Fig. 13). That makes three generators from either family; each generator from one family meets the three from the other, giving nine points of intersection in all. Those first two generators and the first side of the hexagon make a triangle we will call the first triangle; each side of the hexagon has a corresponding triangle, so that the conic is encircled by six triangles (Fig. 14). (Is this a prefiguration of that eye crowned with thorns? If so it is a Pascalian ‘reason of the heart’ for believing that this proof is indeed the one used by
Pascal
.) Among the nine points of intersection mentioned are one corner from each of the six triangles; that leaves three more points of intersection, making a triangle we will call the seventh triangle.
Now look at the first triangle and the one associated with the opposite side of the hexagon, i.e. the fourth triangle (Fig. 15). Each of these triangles lies in a plane defined by two generators, and those two planes meet in a line, which is a side of the seventh triangle. That line meets the plane of the original hexagon, in a point we will call the first crucial point. But the two sides of the hexagon we have been concerned with, lying in the planes of the first and fourth triangle, must meet where those two planes and the plane of the hexagon all meet; that is, in the first crucial point. Similarly, each pair of opposite sides of the hexagon gives rise to a crucial point. These three points all lie in the plane of the
hexagon
and in the plane of the seventh triangle; so they must lie on the line in which those two planes intersect (Fig. 17). Hence,
‘La
Pascale
’
:
the intersections of opposite sides of a hexagon inscribed in a conic lie on a line.
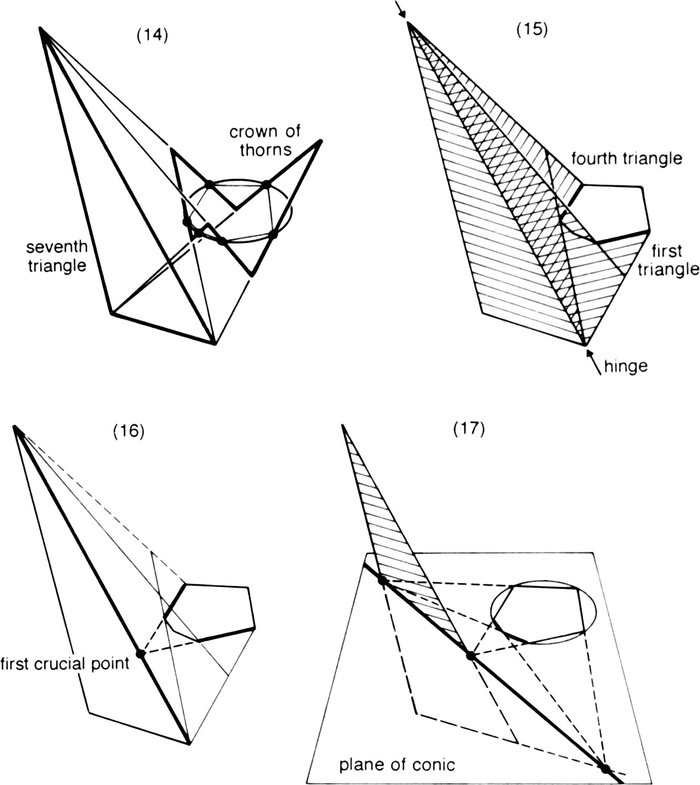
Figs. 14–17. Dandelin’s proof. (Having established the configuration of six lines and their nine points of intersection, we can throw away the hyperboloid.) (14) The crown of thorns and the seventh triangle. (15) The planes of the first, fourth and seventh triangles all hinge on one side of the latter. (The conic is omitted for the moment.) (16) The crucial point where the first and fourth sides of the hexagon meet lies on the side of the seventh triangle. (17) All three
crucial
points lie in the plane of the seventh triangle, and in the plane of the
hexagon
; therefore they lie on the intersection of these two planes.
It was not until the mid-nineteenth century that projective geometry’s independence of and logical anteriority to our familiar schoolbook geometry was established. Euclid’s geometry is ‘
metric
’; the concept of distance is basic to it, and is left undefined within it. Projective geometry starts from hardly more than points, lines and planes, of which all we know is that two points define one line passing through them, two lines (lying in the same plane) intersect in one point, two planes intersect in a line, and so on. Obviously, since Pascal’s definition of a cone mentions the circle it has a secret dependence on the idea of distance, a circle being the locus of a point at a fixed distance from another point, its
centre
. The same is true of Dandelin’s proof above, since it utilizes the hyperboloid which was introduced with the help of a sphere. So these are not purely projective proofs, and it was some time before projective geometry found its own way to these theorems
without
such borrowings from metric geometry. But once the
concepts
of projective geometry have been sufficiently elaborated through theorem after theorem, the idea of distance can be defined in terms of them. Stranger still, the details of the
definition
can be chosen so that the metric geometry that arises is not the familiar one of blackboards; it can be the geometry that describes the properties of figures drawn on a curved surface such as that of a saddle or (with some massaging of difficulties) a sphere. These are all two-dimensional geometries – but three-
dimensional
projective geometry similarly gives rise to three-
dimensional
metric geometries analogous to those of the saddle-shape, the sphere, or the intermediate case of the flat surface. The
three-dimensional
equivalent of this last is the one we know, or think we know, as the Euclidean geometry of everyday life. But the others are logically consistent, if difficult to visualize; these strange ideas of curved spaces were given definite content by geometers of the nineteenth century building on the work of Pascal and his contemporaries. So how do we know what sort of space we
actually
live in? Perhaps if we could see more of it or measure shapes in it more accurately, we would find that on a cosmic scale it is spherical and returns upon itself like a circle or the surface of the globe. Or it may be an infinite space of the sort that terrified
Pascal
, in which case it is either flat (Euclidean) or hyperbolic (which is quite unimaginable in three dimensions, but a hyperboloid
surface
gives a two-dimensional inkling of its twisted nature).