How We Learn (24 page)

Math scores, however, don’t lie.

• • •

Despite its leadership in technical innovation and discovery, the United States has long lagged in math education, usually ranking around ninth or tenth in the world—as measured by performance in eighth graders—far behind countries like South Korea and Finland. Experts and officials are perpetually debating how to close that gap,
and in the late 1980s the nation’s premier organization of math teachers—the National Council of Teachers of Mathematics—convened a meeting of leading educators to review and reshape how the subject was taught.
It was a gargantuan job and, like so many grand-scale efforts,
became bitterly contentious. The central disagreement was over teaching philosophy: Do students learn most efficiently in classes that emphasize the learning of specific problem-solving techniques, like factoring and calculating slope? Or do they benefit more from classes that focus on abstract skills, like reasoning and number sense—knowing, for example, that 2/3 + 3/5 is greater than 1, without having to find a common denominator? The former approach is bottom-up; the latter is top-down.

This being education, the debate was quickly politicized. The top-down camp became “progressives” who wanted children to think independently rather than practice procedures by rote. (This group included many younger teachers and university professors with doctorates in education.) The bottom-up camp became “conservatives” who saw value in the old ways, in using drills as building blocks. (Its core was made up of older teachers and professors of math and engineering.) The math wars, as they were known, caused confusion among many teachers. Math education was virtually devoid of decent research at the time, so neither side had the ammunition to win the argument. The typical experiment involved academics or outside experts descending on a class or school with a novel math, history, or writing curriculum and announcing “improvements” that were hard to interpret, given that the measures (the tests) were often new themselves, and few experiments tracked the teachers’ commitment to the program.

Teachers, then as now, see enough new approaches come and go over time that many become constitutionally skeptical. Plus, this clash over math was (and is) about
philosophies
, and in math of all subjects it is results that matter, not theories. “One of the things you see that’s so baffling, when you’re a new teacher, is that kids who do
great on unit tests—the weekly, or biweekly reviews—often do terribly on cumulative exams on the same material,” Doug Rohrer, who was a high school math teacher in Palo Alto, California, in the late 1980s, told me. “The kids would often blame the test or even blame me explicitly, saying I gave them trick questions.” What made those questions so tricky, explained Rohrer, was that “math students must be able to
choose
a strategy—not just know how to use it—and choosing a strategy is harder when an exam covers many kinds of problems.” For practical teaching issues like this one, the math wars debate was irrelevant.

Rohrer toyed with the idea of developing a different curriculum, one that rejected the idea of teaching in blocks (two weeks on proportions, say, then two weeks on graphs) and instead mixed problems from previously studied topics into daily homework to force students to learn how to choose appropriate solution strategies rather than blindly apply them. To solve a problem, you first have to identify what kind of problem it is. Rohrer was lying on his futon in his studio apartment one day, staring at the ceiling, and thought,
Okay, maybe it’s time to write a textbook of mixed problems
. He soon found out that someone already had.

That someone was a retired Air Force officer turned math teacher in
Oklahoma City. In the 1970s, John H. Saxon was teaching math at Rose State College and growing increasingly exasperated with the textbooks the college used. The books’ approach left students fuzzy on the basics, and quick to forget what they’d just studied. So one day Saxon decided to write out some problem sets of his own, with the goal of building algebra skills differently—i.e., more incrementally—than the standard curriculum. His students improved fast, and soon he was developing entire lesson plans. Between 1980 and 1990, Saxon authored or coauthored twelve math textbooks for kindergarten through high school, plus a couple of college texts. His central innovation was a process of “mixed review.” Each homework assignment included some new technique—solving simultaneous equations,
for example—along with a number of problems from previous lessons, say, solving equations for x. Saxon believed that we grasp a new technique more clearly when using it alongside other, familiar ones, gradually building an understanding of more abstract concepts along the way. His books built a following, mostly among private schools, homeschoolers, and some public districts, and he soon became a lightning rod in the math debate. Saxon was a bottom-up man. He thought the reformers were dangerous and they returned the compliment.

Rohrer wasn’t sure what he thought about the math wars or, for that matter, about Saxon. He does remember picking up the Saxon books and looking at the chapters. They were different, all right. The lessons, in Rohrer’s view, were
not
in logical order. Yet the problems were mixed, from all sorts of different lessons—precisely the approach he thought would help his own students.

He let it drop. Rohrer was ready to walk away from math teaching altogether, and entered graduate school in experimental psychology. It was in 2002—eight years after he finished his degree—that he again began to think about learning. For one thing, he’d read the 1992 Schmidt-Bjork paper on motor and verbal learning. And he returned to the central problem he’d had while teaching high schoolers. His students didn’t need to remember more. Their weakness was distinguishing between problem
types
—and choosing the appropriate strategy. Mixing problem types (he had not yet heard the term interleaving) looked like it might address just this weakness.

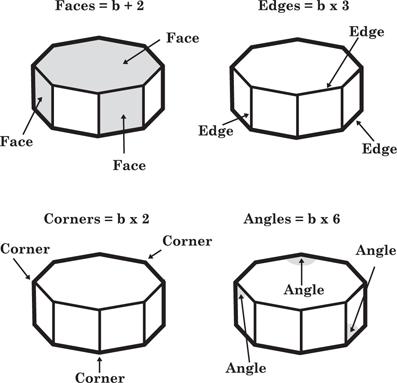
We’ve done well so far to avoid doing any real math in this book, but I think it’s time to break the seal. In the past decade, Rohrer and others have shown in a variety of experiments that interleaving can improve math comprehension across the board, no matter our age. Let’s take a look at one of those studies, just to show how this technique works. We’ll keep it light. This is fourth grade geometry, and a little review never hurt anyone. In 2007, Rohrer and Kelli Taylor, both at the University of South Florida, recruited twenty-four fourth
graders and gave each a tutorial on how to calculate the number of faces, edges, corners, and angles in a prism—given the number of
base sides. The tutorial is self-explanatory and perfectly doable, even for people with math allergies. In the diagrams below,
b
is the number of base sides:

Half the children performed blocked study. They worked eight “face” problems (FFFFFFFF), then eight “edge” problems (EEEEEEEE), eight “corner” problems, and eight “angle” problems in a row, with a thirty-second break in between, all in the same day. The other half worked the same number of each type of problem, only in randomly mixed sets of eight: FCEAECFA, for example, followed by CAAEFECF. The tutorials were identical for each group, and so were the problems. The only difference was the order: sequential in one group and mixed in the other. The next day the children took a test, which included one of each type of problem. Sure enough, those in the mixed-study—interleaved—group did better, and it wasn’t close: 77 to 38 percent.

One fairly obvious reason that interleaving accelerates math learning in particular is that tests themselves—the cumulative exams, that is—are mixed sets of problems. If the test is a potpourri, it helps to make homework the same. There’s much more going on than that, however. Mixing problems during study forces us to identify each type of problem
and
match it to the appropriate kind of solution. We are not only discriminating between the locks to be cracked; we are connecting each lock with the right key. “The difficulty of pairing a problem with the appropriate procedure or concept is ubiquitous in mathematics,” Rohrer and Taylor concluded. “For example, the notorious difficulty of word problems is due partly to the fact that few word problems explicitly indicate which procedure or concept is appropriate. The word problem, ‘If a bug crawls eastward for 8 inches and then crawls northward for 15 inches, how far is it from its starting point?’ requires students to infer the need for the Pythagorean theorem. However, no such inference is required if the word problem appears immediately after a block of problems that explicitly indicate the need for the Pythagorean theorem. Thus, blocked practice can largely reduce the pedagogical
value of the word problem.”

Rohrer puts it this way: “If the homework says ‘The Quadratic Formula’ at the top of the page, you just use that blindly. There’s no need to ask whether it’s appropriate. You know it is before doing the problem.”

The evidence so far suggests that interleaving is likely applicable not just to math, but to almost any topic or skill. Badminton. History (mix concepts from related periods). Basketball (practice around the free throw line, not repeatedly from the line). Biology. Piano. Chemistry. Skateboarding. Blindfolded beanbag throwing, for heaven’s sake. Certainly any material taught in a single semester, in any single course, is a ripe target for interleaving. You have to review the material anyway at some point. You have to learn to distinguish between a holy ton of terms, names, events, concepts, and formulas at exam
time, or execute a fantastic number of perfect bow movements at recital. Why not practice the necessary discrimination skills incrementally, every time you sit down, rather than all at once when ramping up for a final test? As mentioned earlier, many musicians already do a version of mixed practice, splitting their sessions between, say, thirty minutes of scales, thirty minutes of reading new music, and thirty minutes of practicing familiar pieces. That’s the right idea. Chopping that time into even smaller pieces, however—of fifteen minutes, or ten—can produce better results. Remember: Interleaving is not just about review but also discriminating between types of problems, moves, or concepts.

For example, I still take classes when I can in Spanish and Spanish guitar. Every time I look at a list of new vocabulary words, I take that list and combine it with a list of at least as many older words. I do more kinds of mixing with the guitar (maybe because there’s more to mix than words and reading). I do one scale, two or three times, then switch to a piece I know. Then I go back and try again the portions of that just played piece—let’s say it’s Granados’s Spanish Dance Number 5—that I messed up. Play those two times, slowly. Then I’m on to a (different) scale, followed by a few bars of a totally new piece I’m working on. Enough for one pass. I take a break and play a few riffs from the first tune I ever learned, “Stairway to Heaven” (somehow it never gets old), and after that I’m ready to dive into Spanish Classical.

That
is interleaving. And it’s sure to be highly individual, far more effective for some subjects or skills than for others. The important thing to know is that you’re essentially surrounding the new material or new skill set with older stuff, stuff you already know but haven’t revisited in a while, whether it’s a Jimmy Page solo or a painting by Georges Braque.

As I read it, the science suggests that interleaving is, essentially, about preparing the brain for the unexpected. Serious climbers and hikers have a favorite phrase:
It’s not an adventure until something goes wrong
. By wrong they mean
wrong
wrong. A rope snaps; the food supply flies overboard; a bear crawls into the tent. I think interleaving prepares us for a milder form of wrong. Every exam, every tournament, every match, every recital—there’s always some wrinkle, some misplaced calculator or sudden headache, a glaring sun or an unexpected essay question. At bottom, interleaving is a way of building into our daily practice not only a dose of review but also an element of surprise. “The brain is exquisitely tuned to pick up incongruities, all of our work tells us that,” said Michael Inzlicht, a neuroscientist at the University of Toronto. “Seeing something that’s out of order or out of place wakes the brain up, in effect, and prompts the subconscious to process the information more deeply: ‘Why is this here?’ ”

Mixed-up practice doesn’t just build overall dexterity and prompt active discrimination. It helps prepare us for life’s curveballs, literal and figurative.

Part Four