How We Learn (16 page)

Problem Solving

Chapter Six

The Upside of Distraction

The Role of Incubation in Problem Solving

School hits us with at least as many psychological tests as academic ones. Hallway rejection. Playground fights. Hurtful gossip, bad grades, cafeteria food. Yet at the top of that trauma list, for many of us, is the stand-up presentation: being onstage in front of the class, delivering a memorized speech about black holes or the French Resistance or Piltdown Man, and wishing that life had a fastforward button. I’m not proud to admit it, but I’m a charter member of that group. As a kid, I’d open my mouth to begin a presentation and the words would come out in a whisper.

I thought I’d moved beyond that long ago—until early one winter morning in 2011. I showed up at a middle school on the outskirts of New York City, expecting to give an informal talk to a class of twenty or thirty seventh graders about a mystery novel I’d written for kids, in which the clues are pre-algebra problems. When I arrived, however, I was ushered onto the stage of a large auditorium, a school staffer asking whether I needed any audiovisual equipment, computer connections, or PowerPoint. Uh, no. I sure didn’t. The truth
was, I didn’t have a presentation at all. I had a couple of books under my arm and was prepared to answer a few questions about writing, nothing more. The auditorium was filling fast, with teachers herding their classes into rows. Apparently, this was a school-wide event.

I struggled to suppress panic. It crossed my mind to apologize and exit stage left, explaining that I simply wasn’t ready, there’d been some kind of mistake. But it was too late. The crowd was settling in and suddenly the school librarian was onstage, one hand raised, asking for quiet. She introduced me and stepped aside. It was show-time … and I was eleven years old again. My mind went blank. I looked out into a sea of young faces, expectant, curious, impatient. In the back rows I could see kids already squirming.

I needed time. Or a magic trick.

I had neither, so I decided to start with a puzzle. The one that came to mind is ancient, probably dating to the Arab mathematicians of the seventh century. More recently, scientists have used it to study creative problem solving, the ability to discover answers that aren’t intuitive or obvious. It’s easy to explain and accessible for anyone, certainly for middle school students. I noticed a blackboard toward the back of the stage, and I rolled it up into the light. I picked up a piece of chalk and drew six vertical pencils about six inches apart, like a row of fence posts:

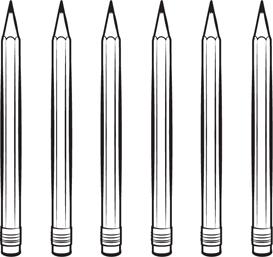
“This is a very famous puzzle, and I promise: Any of you here can solve it,” I said. “Using these pencils, I want you to create four equilateral triangles, with one pencil forming the side of each triangle.” I reminded them what an equilateral triangle is, one with three equal sides:

“So: six pencils. Four triangles. Easy, right? Go.”

The fidgeting stopped. Suddenly, all eyes were on the blackboard. I could practically hear those mental circuits humming.

This is what psychologists call an insight problem, or more colloquially, an aha! problem. Why? Because your first idea for a solution usually doesn’t work … so you try a few variations … and get nowhere … and then you stare at the ceiling for a minute … and then you switch tacks, try something else … feel blocked again … try a totally different approach … and then … aha!—you see it. An insight problem, by definition, is one that requires a person to shift his or her perspective and view the problem in a novel way. The problems are like riddles, and there are long-running debates over whether our ability to crack them is related to IQ or creative and analytical skills. A knack for puzzles doesn’t necessarily make someone a good math, chemistry, or English student. The debate aside, I look at it this way: It sure doesn’t hurt. We need creative ways of thinking to crack any real problem, whether it’s in writing, math, or management. If
the vault door doesn’t open after we’ve tried all our usual combinations, then we’ve got to come up with some others—or look for another way in.

I explained some of this in the auditorium that morning, as the kids stared at the board and whispered to one another. After five minutes or so, a few students ventured up to the blackboard to sketch out their ideas. None worked. The drawings were of triangles with smaller triangles crisscrossing inside, and the sides weren’t equal. Solid efforts all around, but nothing that opened the vault door.

At that point, the fidgeting started again, especially in the back rows. I continued with more of my shtick about math being like a mystery. That you need to make sure you’ve used all available information. That you should always chase down what seem like your stupidest ideas. That, if possible, you should try breaking the problem into smaller pieces. Still, I felt like I was starting to sound to them like the teachers in those old
Charlie Brown
movies (WAH-WAH WAH WAAH WAH), and the mental hum in the room began to dissipate. I needed another trick. I thought of another well-known insight problem and wrote it on the board beneath the chalk pencils:

SEQUENC_

“Okay, let’s take a break and try another one,” I told them. “Your only instruction for this one is to complete the sequence using any letter other than E.”

I consider this a more approachable puzzle than the triangle one, because there’s no scent of math in it. (Anything with geometric shapes or numbers instantly puts off an entire constituency of students who think they’re “not a math person”—or have been told as much.) The SEQUENC_ puzzle is one we all feel we can solve. I hoped not only to keep them engaged but also to draw them in deeper—put them in the right frame of mind to tackle the Pencil
Problem. I could feel the difference in the crowd right away, too. There was a competitive vibe in the air, as if each kid in that audience sensed that this one was within his or her grasp and wanted to be the first to nail it. The teachers began to encourage them as well.

Concentrate, they said.

Think outside the box.

Quiet, you guys in the back.

Pay attention
.

After a few more minutes, a girl near the front raised her hand and offered an answer in a voice that was barely audible, as if she was afraid to be wrong. She had it right, though. I had her come up to the board and fill in the answer—generating a chorus of
Oh man!
and
You’re kidding me, that’s it?
Such are insight problems, I told them. You have to let go of your first ideas, reexamine every detail you’re given, and try to think more expansively.

By this time I was in the fourth quarter of my presentation and still the Pencil Problem mocked them from the board. I had a couple hints up my sleeve, waiting for deployment, but I wanted to let a few more minutes pass before giving anything away. That’s when a boy in the back—the “Pay attention” district—raised his hand. “What about the number four and a triangle?” he said, holding up a diagram on a piece of paper that I couldn’t make out from where I was standing. I invited him up, sensing he had something. He walked onto the stage, drew a simple figure on the board, then looked at me and shrugged. It was a strange moment. The crowd was pulling for him, I could tell, but his solution was not the generally accepted one. Not even close. But it worked.

So it is with the investigation into creative problem solving. The
research itself is out of place in the lab-centric world of psychology, and its conclusions look off-base, not in line with the usual advice we hear, to concentrate, block distractions, and
think
. But they work.

• • •

What
is
insight, anyway? When is the solution to a problem most likely to jump to mind, and why? What is happening in the mind when that flash of X-ray vision reveals an answer?

For much of our history, those questions have been fodder for poets, philosophers, and clerics. To Plato, thinking was a dynamic interaction between observation and argument, which produced “forms,” or ideas, that are closer to reality than the ever-changing things we see, hear, and perceive. To this, Aristotle added the language of logic, a system for moving from one proposition to another—the jay is a bird, and birds have feathers; thus, the jay must have feathers—to discover the essential definitions of things and how they relate. He supplied the vocabulary for what we now call deduction (top-down reasoning, from first principles) and induction (bottom-up, making generalizations based on careful observations), the very foundation of scientific inquiry. In the seventeenth century, Descartes argued that creative problem solving required a retreat inward, to an intellectual realm beyond the senses, where truths could surface like mermaids from the deep.

This kind of stuff is a feast for late night dorm room discussions, or intellectual jousting among doctoral students. It’s philosophy, focused on general principles and logical rules, on discovering “truth” and “essential properties.” It’s also perfectly useless for the student struggling with calculus, or the engineer trying to fix a software problem.

These are more immediate, everyday mental knots, and it was an English intellectual and educator who took the first steps toward answering the most relevant question: What actually happens when the mind is stuck on a problem—and then comes unstuck? What are
the stages of solving a difficult problem, and when and how does the critical insight emerge?

Graham Wallas was known primarily for his theories about social advancement, and for cofounding the London School of Economics. In 1926, at the end of his career, he published
The Art of Thought
, a rambling meditation on learning and education that’s part memoir,
part manifesto. In it, he tells personal stories, drops names, reprints favorite poems. He takes shots at rival intellectuals. He also conducts a wide-ranging analysis of what scientists, poets, novelists, and other creative thinkers, throughout history, had written about how their own insights came about.

Wallas was not content to reprint those self-observations and speculate about them. He was determined to extract a formula of sorts: a
specific series of steps
that each of these thinkers took to reach a solution, a framework that anyone could use. Psychologists at the time had no language to describe these steps, no proper definitions to work with, and thus no way to study this most fundamental human ability. To Wallas, this was appalling. His goal was to invent a common language.

The raw material Wallas cites is fascinating to read. For example, he quotes the French mathematician Henri Poincaré, who had written extensively about his experience trying to work out the properties of a class of forms called Fuchsian functions. “Often when one works at a hard question, nothing good is accomplished at the first attack,” Poincaré had observed. “Then one takes a rest, longer or shorter, and sits down anew to the work. During the first half hour, as before, nothing is found, and then all of a sudden the decisive idea
presents itself to the mind.” Wallas also quotes the German physicist Hermann von Helmholtz, who described how new ideas would bubble up after he’d worked hard on a problem and hit a wall: “Happy ideas come unexpectedly, without effort, like an inspiration,” he wrote. “So far as I am concerned, they have never come to me when my mind was fatigued, or when I was at my working table … they came
particularly readily during the slow ascent of wooded
hills on a sunny day.” The Belgian psychologist Julien Varendonck traced his insights to daydreaming after a period of work, sensing that “there is something going on in my foreconsciousness which must be in direct relation to my subject. I ought to stop reading for a little while and let it come to the surface.”