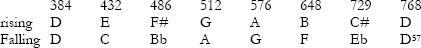Grid of the Gods (45 page)
Authors: Joseph P. Farrell,Scott D. de Hart

Musical Brahmins and Babylonian “Star of David”
46
The significance of all this is that music and its mathematical codes, in McClain’s view, played an inevitable role in the emergence of monotheism:
Monotheism took as its God not the Great God 60(actually written in Babylonian-Sumerian as a large ONE), but the irreducible unity itself, that is, the unity whose multiplicity creates all the diversity of number, that unity which alone can subdivide prime numbers, the active agents of all creation.
47
And of these, as we see from the previous page, the numbers 3 and 5 are the first two and most important prime numbers in the musical metaphor.
In other words, the ancient mathematicians performed what geometers would call a
rotation,
revealing a connection to another metaphorical mountain, the sacred tectratys of Pythagoreanism
:
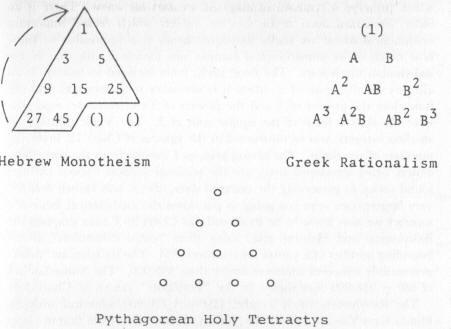
McClain’s Musical Evolution of Monotheism
48
We will reserve comment on all the esoteric and physical principles embodied in the Pythagorean tectratys for chapter twelve. For now, it should be noted that, like the musical circle of tones itself, we have returned to that musical-topological metaphor that began the process we discovered at Angkor Wat, but now the metaphor has taken on an added richness, for specific numerical and musical functions have now been ascribed to the original primary “tripartition” or differentiation.
1. Babylonian and Hebrew Flood Chronologies
There is another backdrop against which the ancient physics of the grid must be viewed, and that is the Platonic allegory of Atlantis and of the Flood itself, an account that McClain, with much humor and accuracy, says is a “kind of Pythagorean Grand Opera, complete with an all-star cast, a water show, dazzling scenery, and a tragic finale.”
49
Yet, even here one finds that there are codes within the texts.
For example, there are hidden correspondences between the Hebrew and Babylonian chronologies of the Flood, correspondences that point to deeper numerical codes. McClain observes that the famous scholar of comparative mythologies, Joseph Campbell,
… discovered a correlation between the 432,000 years from the creation to the flood in Babylonian mythology and the 1,656 years from the creation of Adam to the flood in the Hebrew account. Campbell points out that these numbers have a common factor of 72, and that 1656/72 is 23. Now 23 Jewish years of 365 days plus five extra days for leap years equals 8,400 days or 1,200 seven-day weeks; multiplying by 72 to find the number of Jewish seven-day weeks in 1,656 (= 23 x 72) years yields 86,400 (1200 x 72). But the number 86,400 is 432,000/5, i.e., the number of Babylonian five- day weeks to the flood. Thus there is
no necessary contradiction
whatever in these different flood chronologies.
50
To put it differently, it is possible that the standard views of conservative biblical scholars as to the relative recentness of the Deluge are thrown into a cocked hat, and that the actual meaning of the biblical numerical codes is that the Deluge occurred much farther back in time, in a context or chronological framework commensurate with its antiquity in Mesopotamian myths.
2. Babylonian Mathematics: Clues to a Higher-Dimensional Physics?
In this context, a closer look at the sexagesimal system of ancient Sumer and Babylon are in order, for as has been seen, various
numbers are ascribed to various gods in the pantheon. But there is another clue in Mesopotamian numbers, a clue that, oddly, resembles the modern numerical notations for higher-dimensional geometric objects: “In the sexagesimal system, 450,000 would be written as 2,5, meaning 2 x 603 + (5 x 602), perhaps a pun on Marduk = 25.”
51
Note that in this system of notation, each number in {2,5} stands for that number in connection with some function that is a power of 60. One can, notes McClain, have a series of such numbers, such as {8,0,0} and so on.
52
It is important to note what this notation means, for cubing and squaring a number — e.g. x3 and x2 — are, of course,
geometrical functions describing objects in two or three spatial dimensions
. Thus, the notation {2,5} mentioned above could be written this way more abstractly as {x, y}, and since the first number is multiplied by the cubic power of 60, and the second by the squared power of 60, the notation really would look like this:

We can therefore imagine
extending
this notation to {x,y,z}, and extending the powers of 60 with which each number is multiplied, e.g. {(x ⋅ 604) + (y ⋅ 603) + (z ⋅ 602)}; in other words, notations such as {8,0,0}, which are also within the realm of possibility in ancient Mesopotamian notation, conceivably may be understood as representing powers of 60
greater
than the cubic, that is to say, as geometric and numerical representations of objects in
four
or more dimensions.
To state it as succinctly as possible, the very structure of ancient Mesopotamian numerical notation implies a basic familiarity with hyper-dimensional geometries and the basic mathematical techniques for describing objects in four or more spatial dimensions. Indeed, as we shall discover in chapter 13,
the exact same notation convention began to
be used in nineteenth century geometrical techniques for describing objects in four or more dimensions!
53
This contains a further, and very suggestive, implication, for it is to be noted that the Sumerian-Babylonian gods may be described by such notation. In other words,
the gods were being described peculiar union of physics and religion, as hyper-dimensional entities or objects.
54
This new twist upon the “unified intention of symbol” we will encounter again in the next part of this book in conjunction with the Egyptian interpretation of this paleophysics of the physical medium, and its conjunction with religious cosmology. It is, however, a heritage that we have discovered is common to ancient Vedic India as well as Mesopotamia, and we have encountered suggestive parallels between Mesopotamian myths and those of Meso-America. It was, to paraphrase McClain, in India, Mesopotamia, Egypt and even Meso- America, that one is able “to watch the birth of the gods in the minds of musical poets and discover that continuity of tradition which maintains a perfect unity between music, mathematics, and metaphysics.”
55
With Plato, the final step was taken, as the physics of the celestial harmonies and the gods was transformed into a technique of social engineering and political theory.
56
The ancient classical world had, in other words, moved quickly to outline all the implications of this musico-physical-metaphysical legacy that it had inherited, even though it may not have fully understood those implications, nor raised the technology to match in deed what its mythologies recorded.
3. Mesopotamian Music and the Fine Structure Constant
But does all this musical numerology actually contain any clue that the ancients were passing on a legacy that contained within it the seeds of a lost knowledge of a much deeper physics?
There is indeed one such clue, and it’s a whopper.
The Greeks, as noted above, inherited this musical-metaphysical legacy from Plato, who in turn gained it from the Pythagoreans and Mesopotamia. One may also point out that Plato was clear — in his “Atlantean dialogues,” the
Timeus
and
Critias —
that there was also an Egyptian influence at work. All this was in turn encoded by Plato in many dialogues as a political theory, as a
means of social engineering.
Various “cities” are worked out — including Atlantis and Athens — along different numerical lines. In these attempts to divine the musical proportions of the “best” city, Plato proposes the city Callipolis, his
‘absolutely best’ city — his ‘celestial city,’ the
diatonic
scale sung by the Sirens in his planetary model — seven numbers required for the diatonic scale produce all eleven tones.
McClain observes that within this octave-numerical scheme, that the largest “genetic element is 3
6
, or 729.
58
That number — 729 — may be one of the most significant in all of physics, for it is the decimal coefficient of the Fine Structure Constant, typically given a fractional value of 1/137 and usually denoted, coincidentally, and perhaps ironically enough, by the Greek letter alpha, α, for when one carries out the function of dividing 1 by 137, the result is .00729927007, an approximate harmonic of 729.
59
Of course, the presence of only one occurrence of this coefficient does not mean that the Greeks — or for that matter those from whom they inherited their knowledge — were aware of this significance of this number. But as we shall discover in the next section on Egypt, there is strong and suggestive evidence that whatever Very High Civilization as preceded those cultures of the classic era(i.e., the Vedic, Mesopotamian, Egyptian and Greek
civilizations), that civilization
did
know of the existence of these and other constants of modern physical mechanics, millennia before their (re-)discovery in our own era.
Why would the preservation of the numerical value of the fine structure constant, particularly in a musical-political context, be so significant? The answer lies in the deeply mysterious nature of the constant itself. First discovered in 1916 by physicist Arnold Sommerfeld, the constant is essentially a
dimensionless
constant — effectively, a scalar in mathematical terms, or a “pure magnitude” — possessing the same value in all systems or units of measure, and measuring the strength of electromagnetic coupling. But the problem is, while the constant “fits” the rest of physics like a glove, its own origins are so unique and inscrutable that it has puzzled physicists ever since. No less a physicist than Feynmann felt compelled to comment on its almost mystical nature and attraction for physicists ever since its first discovery:
It has been a mystery since it was discovered more than fifty years ago, and all good theoretical physicists put this number
60
up on their wall and worry about it. Immediately you would like to know where this number for a coupling comes from; is it related to π or perhaps to the base of natural logarithms? Nobody knows. It’s one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the “hand of God” wrote that number, and “we don’t know how He pushed his pencil.” We know what kind of a dance to do experimentally to measure this number very accurately, but we don’t know what kind of dance to do with the computer to make this number come out, without putting it in secretly!
61