Grid of the Gods (41 page)
Authors: Joseph P. Farrell,Scott D. de Hart

There is loosely corroborating support for the antiquity of this site from Mayan texts, Aztec mythology and ritual practices. Peter Tompkins notes that the Aztecs and Mayans may have inherited the practice of human sacrifice from some contact with the Phoenicians, who were the ultimate practitioners of child sacrifice. Citing the work of archaeologist Hugh Fox, Tompkins notes that the practice of sacrifice in the Old World, emerged after the Flood in conjunction with an attempt to appease the gods and ward off another catastrophe, a conjunction of ideas also apparently at work in Mayan and Aztec thinking.
27
The Mayan Troano Codex spoke of a great catastrophe that had sunk an island in the Atlantic Ocean “extending eastward in a crescent as far as the Canary Islands” ca. 9937 BC.
28
The close proximity of this date to the 10,500 BC date mentioned elsewhere should be noted, for again it suggests that one is looking at a common cultural inheritance spanning the globe.
It is fairly certain that the Pyramid of the Sun at Teotihuacan was once dedicated to the Sovereign Plumed Serpent, Quetzcoatl, for the Mexican archaeologist Batras discovered many worked shells depicting snakes on and around the pyramid during his excavations of the site in the early twentieth century.
29
However, there was a much deeper mystery concerning the Pyramid of the Sun, one suggesting that the structure was conceived for some machine-like function:
An unpublished find on the fifth level has never been adequately explained. While the Sun Pyramid was first being probed by Batras in 1906, an archeologist working with him reported a thick sheet of mica covering the top of the fifth body. This material was apparently carried away during the course of the restoration.
Coincidentally, a “Temple of Mica” was also found to the south of the Sun Pyramid about 350 meters down the Way of the Dead, where the local guard will still let one peek through a glass panel at
the floor covered with mica slabs. Mica has two outstanding characteristics: high electrical resistance and opaqueness to fast neutrons. Hence it acts as an insulator or nuclear reaction moderator, which raises the question as to why two separate areas of Teotihuacan were covered with mica.
30
In addition to these properties, mica may also be used in the manufacture of capacitors and as an insulator in high voltage machines.
While mica
was
used in ancient times for purposes other than these modern ones, its presence in the Pyramid of the Sun, plus the structure’s possible antiquity, suggests that one may not too easily close the door on the possibility that its presence served some functional purpose. In this case, there are three possible properties:
1) as an electrical insulator;
2) as a dielectric in a capacitor; and
3) as a nuclear moderator.
Given these choices, one may speculate that perhaps the first two usages were intended by the structure’s builders, but we will have to reserve any further commentary about this structure and its possible functional purpose for a possible future sequel on the Grid.
Munck notes that the Teotihuacan-Giza parallelism is quite acute, for the three main pyramids of Giza, Mycerinus, Cephren, and the Great Pyramid itself, are exact analogies to the Moon Pyramid, the Sun Pyramid, and the “Quetzlcoatl” complex at Teotihuacan.
31
And both these places with their three main structures are, as most know, laid out according to the patterns of the stars of the constellation Orion’s “belt.” For our purposes, however, we make an assumption, and note one thing. The assumption - which will be argued in chapter thirteen - is that we are looking an
machines
designed to engineer a hyper-dimensional physics. Once we have granted that assumption, then something immediately follows: Giza and Teotihuacan are designed according to the same basic plan, that is to say, they could be coupled oscillators to each other in some fashion.
Munck makes some crucial observations regarding the most massive structure at Teotihuacan, the Pyramid of the Sun, and these play directly into our assumptions that we are looking at “hyper- dimensional engineering.” A glance at this structure in side elevation, courtesy of the detailed line drawings of engineer Hugh Harleston, Jr., is in order.
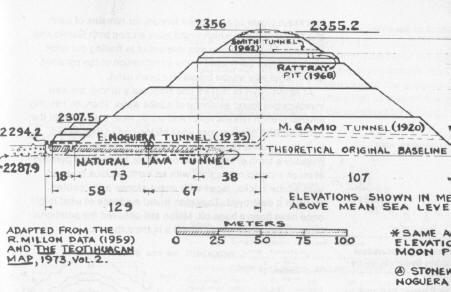
Hugh Harleston Jr’s Side Elevation view of the Pyramid of the Sun.
Note that all measures are given in meters.
32
Note, says Munck, that the pyramid is
deliberately
offset, much like the “temples” of Tikal.
33
The offset, moreover, occurs on the level of the second terrace, and of all five terraces, only the lower two are centered. Following his method of counting faces and sides, this gives Munck the following interesting set of numbers:
1) Centered terraces: 2
2) Faces on one side elevation of the pyramid 6
3) Number of terraces 5
4) Offset faces on one side elevation 4
34
Taking each of these numbers times π times each other, e.g., 2π x 4π x 5π x 6π yields 23,378,.18184, which translates to 19o 41’ when converted to normal degrees measures.
35
This is, of course, our first clue that we are indeed dealing with a hyper-dimensional structure, for the first of the Platonic solids, a tetrahedron, is circumscribed in a sphere, with on vertex on the rotational axis, will have the other three vertices touching at 19 degrees 47 minutes north or south latitude, depending upon which rotational pole the fourth vertex is positioned. And was we shall see in chapter thirteen, this is a profound clue to hyper-dimensional geometries, to geometries done in more than three spatial dimensions.
Here we must begin, however, to take some issue with Munck, for from a strictly geometrical perspective, there is no difference between
terraces
and
faces;
for a geometer, they are both the same. Additionally, we would have to multiply his numbers by four, since there are four sides to the structure (remember, the terraces count as
one
face since they extend around the entire structure, so we do
not
multiply them by four).
We would get the following adjusted table of numbers:
1) Centered faces (i.e., faces and terraces) 10
2) Offset faces (i.e., faces and terraces) 19
3) total faces (i.e., all faces and terraces) 29
Note that we are counting only the faces of the basic structure, not the faces that would be added from the staircases and so on. Now there are two more numbers that should be added to this list:
corners
and
edges:
4) Number of corners, or vertices 44
5) Number of edges 78
As we shall see in chapter thirteen, these sorts of numbers are strongly suggestive of strange sorts of hyper-dimensional objects
called compounds, though as we shall also see, there is a problem. But nonetheless, these sorts of numbers permit us to offer yet another speculation about what kind of machines they are:
by dint of the numbers of faces edges, and vertices embodied in their numbers, these objects appear to be constructed as three-dimensional analogues of higher-dimensional objects, as
resonators
of them.
If this sounds like the flights of purest science fiction fantasy, it isn’t, for the mathematician Hugh Harleston Jr, whose diagrams we have been utilizing, noticed the same thing about the musical and tetrahedral properties of Teotihuacan, and its relationship to the physics of the medium:
The angles and perspectives in the Teotihuacan layout appear to Harleston to show the framework of an integrated earth and heaven - along with the megaspace of the heavens above - as being the work of a master mathematician. To Harleston the messages of Teotihuacan point to a new way of looking at time and space, and to some new source of energy from the cosmos, some new field fabric that our science has not yet isolated…
Harleston says that once the student at Teotihuacan learned the important values of thirds, sevenths, and ninths, that squares and sqaure roots were basic mathematical tools, the next step was to understand the relationship of two simple geometric solids: the sphere and the tetrahedron.
It was some time before Harleston found the clue to a tetrahedral geometry incorporated into the Teotihuacan complex, but he finally found it in the dimensions of the Pyramid of the Sun. Unlike the Pyramid of Cheops, which is a very exact scale model of the Northern Hemisphere (with the apex as the North Pole, the base as the equator, and its perimeter equal to one-half minute of arc), the Sun Pyramid does not fit such a system; it does, however, very accurately give the entire surface of the earth.
36
Why is this so? because as we have already seen, the tetrahedral number of 19.5 is already approximated in the structure in terms of its number of faces and π. But there is also
another
way it is incorporated:
Oddly, or coincidentally, the relation between a tetrahedron and a sphere constitutes the thrust of the work of Buckminster Fuller, who, in his book
Synergetics
, maintains that the tetrahedron gives the basic mathematical blueprint for the universe.
From what he calls his “isotropic vector matrix” Fuller obtains a constant of √9/8, which comes to `1.065066, so close to Harleston’s 1.059 constant that it fits the Teotihuacan complex virtually as well.
37
This tetrahedral redundancy that was built into Teotihuacan was not lost on Harleston:
Pointing out that the carbon atom - which is the basic building block from which the material bodies of all living organisms are made - is a regular tetrahedron, and that the water molecule has characteristics that conform to the tetrahedral structure, Harleston concludes that the fundamental message conveyed by the Teotihuacanos is that the physical universe is tetrahedral from the microscopic level of the atom all the way up to the macroscopic level of the galaxies on a scale of vibrations
in which man stands about the center
. Man would thus have built into him, as suggested by Pythagoras and Plato, the tool for unlocking the geometry of the cosmos and recovering the knowledge of his role in the scheme.
38
Those numbers, 9 and 8, and those mystics, Pythagoras and Plato, we shall encounter again in the next chapter, and man’s unique position, as the microcosm and mediator in this cosmic, tetrahedral temple, we shall have much occasion to comment on in the fourth part of this book in connection with Egypt.
That positioning of man somewhere in the
middle
of all this physics, however, does suggest one final, significant clue as to why human sacrifice was practiced by
some
with a possible understanding of this physics, of the analogical nature of consciousness itself, and of the analogical view of the physical medium which the ancients held, for standing midway between the physics of the very small and the very large, man himself was the natural and most efficient
resonator
of all those things. For those intending to exercise power and influence
over the medium via its interface with consciousness, through the instrumentality of shock and emotional trauma induced within it by brutality and sacrifice, the selection of mankind is in some sense the manifestation of a twisted logic and a twisted music.
39
But the original music, echoed from the Vedas down through Mesopotamia and Egypt, must now come into view, to see just how twisted that logic really was.
Notes
1
Anselm of Canterbury,
Cur Deus Homo
(
Why the God-man?
), Preface. http://www.ewtn.com/library/CHRIST/CURDEUS.HTM.