Gödel, Escher, Bach: An Eternal Golden Braid (26 page)

Then comes the B-section. With the inversion of the theme for our melody, we begin in D as if that had always been the tonic-but we modulate back to G after all, which means that we pop back into the tonic, and the B-section ends properly. Then that funny repetition takes place, jerking us without warning back into D, and letting us return to G

once more. Then that funny repetition takes place, jerking us without warning back into D, and letting us return to G once more.

The psychological effect of all this key shifting-some jerky, some smooth-is very difficult to describe. It is part of the magic of music that we can automatically make sense of these shifts. Or perhaps it is the magic of Bach that he can write pieces with this kind of structure which have such a natural grace to them that we are not aware of exactly what is happening.

The original
Little Harmonic Labyrinth
is a piece by Bach in which he tries to lose you in a labyrinth of quick key changes. Pretty soon you are so disoriented that you don't have any sense of direction left-you don't know where the true tonic is, unless you have perfect pitch, or like Theseus, have a friend like Ariadne who gives you a thread that allows you to retrace your steps. In this case, the thread would be a written score. This piece-another example is the Endlessly Rising Canon-goes to show that, as music listeners, we don't have very reliable deep stacks.

Recursion in Language

Our mental stacking power is perhaps slightly stronger in language. The grammatical structure of all languages involves setting up quite elaborate push-down stacks, though, to be sure, the difficulty of understanding a sentence increases sharply with the number of pushes onto the stack. The proverbial German phenomenon of the "verb-at-the-end", about which

Droll tales of absentminded professors who would begin a sentence, ramble on for an entire lecture, and then finish up by rattling off a string of verbs by which their audience, for whom the stack had long since lost its coherence, would be totally nonplussed, are told, is an excellent example of linguistic pushing and popping. The confusion among the audience out-of-order popping from the stack onto which the professor's verbs been pushed, is amusing to imagine, could engender. But in normal ken German, such deep stacks almost never occur-in fact, native speaker of German often unconsciously violate certain conventions which force verb to go to the end, in order to avoid the mental effort of keeping track of the stack. Every language has constructions which involve stacks, though usually of a less spectacular nature than German. But there are always of rephrasing sentences so that the depth of stacking is minimal.

Recursive Transition Networks

The syntactical structure of sentences affords a good place to present a of describing recursive structures and processes: the
Recursive Transition Network
(
RTN
). An
RTN
is a diagram showing various paths which can be followed to accomplish a particular task.

Each path consists of a number of
nodes
, or little boxes with words in them, joined by
arcs
, or lines with arrows. The overall name for the
RTN
is written separately at the left, and the and last nodes have the words
begin
and
end
in them. All the other nodes contain either very short explicit directions to perform, or else name other
RTN'
s
. Each time you hit a node, you are to carry out the direct inside it, or to jump to the
RTN
named inside it, and carry it out.

Let's take a sample
RTN
, called
ORNATE NOUN
, which tells how to construct a certain type of English noun phrase. (See Fig. 27a.) If traverse
ORNATE NOUN

purely horizontally, we
begin'
, then we create
ARTICLE
, an
ADJECTIVE
, and a
NOUN
, then we
end
. For instance, "the shampoo" or "a thankless brunch". But the arcs show other possibilities such as skipping the article, or repeating the adjective. Thus we co construct "milk", or "big red blue green sneezes", etc.

When you hit the node
NOUN
, you are asking the unknown black I called
NOUN

to fetch any noun for you from its storehouse of nouns. This is known as a
procedure
call
, in computer science terminology. It means you temporarily give control to a
procedure
(here,
NOUN
) which (1) does thing (produces a noun) and then (2) hands control back to you. In above
RTN
, there are calls on three such procedures:
ARTICLE
,
ADJECTIVE
and
NOUN
. Now the
RTN
ORNATE NOUN
could itself be called from so other
RTN
-for instance an
RTN
called
SENTENCE
. In this case,
ORNATE NOUN

would produce a phrase such as "the silly shampoo" and d return to the place inside
SENTENCE
from which it had been called. I quite reminiscent of the way in which you resume where you left off nested telephone calls or nested news reports.

However, despite calling this a "recursive transition network", we have

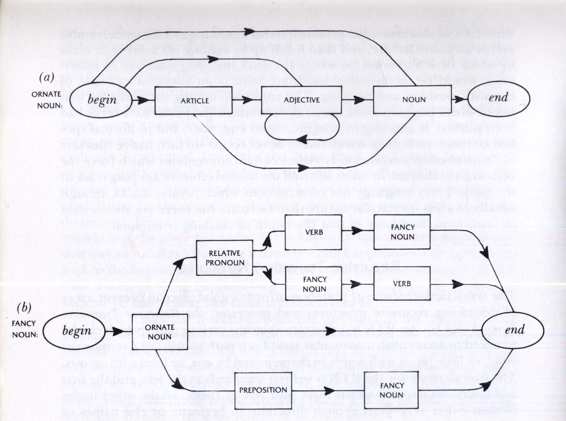
FIGURE 27. Recursive Transition Networks for
ORNATE NOUN
and
FANCY NOUN
.

not exhibited any true recursion so far. Things get recursive-and seemingly circular-when you go to an
RTN
such as the one in Figure 27b, for
FANCY NOUN
. As you can see, every possible pathway in FA
NCY NOUN
involves a call on
ORNATE NOUN
, so there is no way to avoid getting a noun of some sort or other. And it is possible to be no more ornate than that, coming out merely with "milk" or "big red blue green sneezes". But three of the pathways involve
recursive
calls on
FANCY NOUN
itself. It certainly looks as if something is being defined in terms of itself. Is that what is happening, or not?

The answer is "yes, but benignly". Suppose that, in the procedure
SENTENCE
, there is a node which calls
FANCY NOUN
, and we hit that node. This means that we commit to memory (viz., the stack) the location of that node inside
SENTENCE
, so we'll know where to return to-then we transfer our attention to the procedure
FANCY NOUN
.

Now we must choose a pathway to take, in order to generate a
FANCY NOUN
. Suppose we choose the lower of the upper pathways-the one whose calling sequence goes:
ORNATE NOUN; RELATIVE PRONOUN; FANCY NOUN; VERB.

So we spit out an
ORNATE NOUN
: "
the strange bagels
"; a
RELATIVE NOUN
:

"
that
"; and now we are suddenly asked for a
FANCY NOUN
. B are in the middle of
FANCY NOUN
! Yes, but remember our executive was in the middle of one phone call when he got another one. He n stored the old phone call's status on a stack, and began the new one nothing were unusual. So we shall do the same.

We first write down in our stack the node we are at in the outer call on
FANCY

NOUN
, so that we have a "return address"; then we jump t beginning of
FANCY NOUN

as if nothing were unusual. Now we h~ choose a pathway again. For variety's sake, let's choose the lower pat]
ORNATE NOUN; PREPOSITION; FANCY NOUN
. That means we produce an
ORNATE NOUN
(say "
the purple cow
"), then a
PREPOSITION

(say “
without
"), and once again, we hit the recursion. So we hang onto our hats descend one more level. To avoid complexity, let's assume that this the pathway we take is the direct one just
ORNATE NOUN.
For example: we might get "
horns
". We hit the node
END
in this call on
FANCY NOUN
which amounts to popping out, and so we go to our stack to find the return address. It tells us that we were in the middle of executing
FANCY NOUN
one level up-and so we resume there. This yields "
the purple cow
without horns
". On this level, too, we hit END, and so we pop up once more, this finding ourselves in need of a
VERB
-so let's choose "
gobbled
". This ends highest-level call on
FANCY NOUN
, with the result that the phrase

"the strange bagels that the purple cow without horns gobbled"

will get passed upwards to the patient
SENTENCE
, as we pop for the last time.

As you see, we didn't get into any infinite regress. The reason is tl least one pathway inside the
RTN FANCY NOUN
does not involve recursive calls on
FANCY

NOUN
itself. Of course, we could have perversely insisted on always choosing the bottom pathway inside
FANCY NOUN
then we would never have gotten finished, just as the acronym "
GOD
” never got fully expanded. But if the pathways are chosen at random, an infinite regress of that sort will not happen.

"Bottoming Out" and Heterarchies

This is the crucial fact which distinguishes recursive definitions from circular ones. There is always some part of the definition which avoids reference, so that the action of constructing an object which satisfies the definition will eventually "bottom out".

Now there are more oblique ways of achieving recursivity in
RTN
s than by self-calling. There is the analogue of
Escher's Drawing
(Fig. 135), where each of two procedures calls the other, but not itself. For example, we could have an
RTN
named
CLAUSE
, which calls
FANCY NOUN
whenever it needs an object for a transitive verb, and conversely, the u path of
FANCY NOUN
could call
RELATIVE PRONOUN
and then
CLAUSE

whenever it wants a relative clause. This is an example of indirect recursion. It is reminiscent also of the two-step version of the Epimenides paradox.

Needless to say, there can be a trio of procedures which call one another, cyclically-and so on. There can be a whole family of
RTN
's which are all tangled up, calling each other and themselves like crazy. A program which has such a structure in which there is no single "highest level", or "monitor", is called a heterarchy (as distinguished from a hierarchy). The term is due, I believe, to Warren McCulloch, one of the first cyberneticists, and a reverent student of brains and minds.

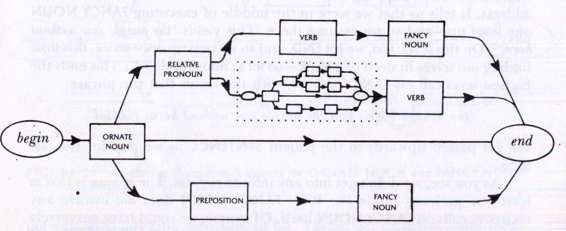
Expanding Nodes

One graphic way of thinking about
RTN
's is this. Whenever you are moving along some pathway and you hit a node which calls on an
RTN
, you "expand" that node, which means to replace it by a very small copy of the
RTN
it calls (see Fig. 28). Then you proceed into the very small
RTN
,

FIGURE 28. The
FANCY NOUN RTN
with one node recursively expanded
When you pop out of it, you are automatically in the right place in the big one. While in the small one, you may wind up constructing even more miniature
RTN
's. But by expanding nodes only when you come across them, you avoid the need to make an infinite diagram, even when an
RTN
calls itself.

Expanding a node is a little like replacing a letter in an acronym by the word it stands for. The "
GOD
" acronym is recursive but has the defect-or advantage-that you must repeatedly expand thèG'; thus it never bottoms out. When an
RTN
is implemented as a real computer program, however, it always has at least one pathway which avoids recursivity (direct or indirect) so that infinite regress is not created. Even the most heterarchical program structure bottoms out-otherwise it couldn't run! It would just be constantly expanding node after node, but never performing any action.