Gödel, Escher, Bach: An Eternal Golden Braid (101 page)

FIGURE 105. Srinivasa Ramanujan and

one of his strange Indian melodies.

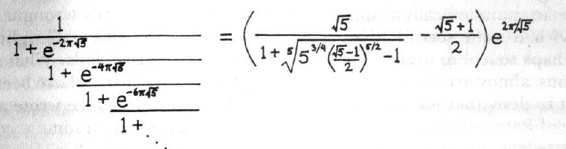
results together in a packet of papers, and sent them all to the, unforewarned Hardy with a covering letter which friends helped him express

in English. Below are some excerpts taken from Hardy's description of his reaction upon receiving the bundle:

... It soon became obvious that Ramanujan must possess much more general theorems and was keeping a great deal up his sleeve.... [Some formulae]defeated me completely; I had never seen anything in the least like them before. A single look at them is enough to show that they could only be written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them. Finally ... the writer must be completely honest, because great mathematicians are commoner than thieves or humbugs of such incredible skill2

What resulted from this correspondence was that Ramanujan came to England in 1913, sponsored by Hardy; and then followed an intense collaboration which terminated in Ramanujan's early demise at age thin thirty-three from tuberculosis.

Ramanujan had several extraordinary characteristics which set him apart from the majority of mathematicians. One was his lack of rigor. Very often he would simply state a result which, he would insist, had just come to

him from a vague intuitive source, far out of the realm of conscious probing. In fact, he often said that the goddess Namagiri inspired him in his dreams. This happened time and again, and what made it all the more mystifying-perhaps even imbuing it with a certain mystical quality-was the fact that many of his "intuition-theorems" were wrong. Now there is a curious paradoxical effect where sometimes an event which you think could not help but make credulous people become a little more skeptical, actually has the reverse effect, hitting the credulous ones in some vulnerable spot of their minds, tantalizing them with the hint of some baffling irrational side of human nature. Such was the case with Ramanujan's blunders: many educated people with a yearning to believe in something of the sort considered Ramanujan's intuitive powers to be evidence of a mystical insight into Truth, and the fact of his fallibility seemed, if anything, to strengthen, rather than weaken, such beliefs.

Of course it didn't hurt that he was from one of the most backward parts of India, where fakirism and other eerie Indian rites had been practiced for millennia, and were still practiced with a frequency probably exceeding that of the teaching of higher mathematics. And his occasional wrong flashes of insight, instead of suggesting to people that he was merely human, paradoxically inspired the idea that Ramanujan's wrongness always had some sort of "deeper rightness" to it-an "Oriental" rightness, perhaps touching upon truths inaccessible to Western minds. What a delicious, almost irresistible thought!

Even Hardy-who would have been the first to deny that Ramanujan had any mystical powers-once wrote about one of Ramanujan's failures, "And yet I am not sure that, in some ways, his failure was not more wonderful than any of his triumphs."

The other outstanding feature of Ramanujan's mathematical personality was his

"friendship with the integers", as his colleague Littlewood put it. This is a characteristic that a fair number of mathematicians share to some degree or other, but which Ramanujan possessed to an extreme. There are a couple of anecdotes which illustrate this special power. The first one is related by Hardy:

I remember once going to see him when he was lying ill at Putney. I had ridden in taxi-cab No. 1729, and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. "No," he replied, "it is a very interesting number; it is the smallest number expressible as a sum of two cubes in two different ways." .1 asked him, naturally, whether he knew the answer to the corresponding problem for fourth powers; and he replied, after a moment's thought, that he could see no obvious example, and thought that the first such number must be very large.'

It turns out that the answer for fourth powers is:

635318657 = 134 + 1334 = 1584 + 594

The reader may find it interesting to tackle the analogous problem for squares, which is much easier.

It is actually quite interesting to ponder why it is that Hardy immediately jumped to fourth powers. After all, there are several other reasonably natural generalizations of the equation

u3 + v3 = x3 + y3

along different dimensions. For instance, there is the question about representing a number in three distinct ways as a sum of two cubes:

r3 + 3 = u3 + v3 = x3 + y3

Or, one can use three different cubes:

u3 + v3 + w3 = x3 + y3 + z3,

Or one can even make a Grand Generalization in all dimensions at once: r4 + s4 + t4 = u4 + v4 + w4 = x4 + v4 + z4

There is a sense, however, in which Hardy's generalization is "the most mathematician-like". Could this sense of mathematical esthetics ever be programmed?

The other anecdote is taken from a biography of Ramanujan by his

countryman S. R. Ranganathan, where it is called "Ramanujan's Flash". It is related by a Indian friend of Ramanujan's from his Cambridge days, Dr. P. C. Mahalanobis.

On another occasion, I went to his room to have lunch with him. The First World War had started some time earlier. I had in my hand a copy of the monthly "Strand Magazine" which at that time used to publish a number of puzzles to be solved by readers. Ramanujan was stirring something in a pan over the fire for our lunch. I was sitting near the table, turning over the pages of the Magazine. I got interested in a problem involving a relation between two numbers. I have forgotten the details; but I remember the type of the problem. Two British officers had been billeted in Paris in two different houses in a long street; the door numbers of these houses were related in a special way; the problem was to find out the two numbers. It was not at all difficult. I got the solution in a few minutes by trial and error.

MAHALANOBIS (in a joking way): Now here is a problem for you.

RAMANUJAN: What problem, tell me.'(He went on stirring the pan.) I read out the question from the "Strand Magazine".

RAMANUJAN: Please take down the solution. (He dictated a continued fraction.) The first term was the solution which I had obtained. Each successive term represented successive solutions for the same type of relation between two numbers, as the number of houses in the street would increase indefinitely. I was amazed.

MAHALANOBIS: Did you get the solution in a flash?

RAMANUJAN: Immediately I heard the problem, it was clear that the Solution was obviously a continued fraction; I then thought, "Which continued fraction?" and the answer came to my mind. It was just as simple as this.'

Hardy, as Ramanujan's closest co-worker, was often asked after

Ramanujan's death if there had been any occult or otherwise exotically flavored elements to Ramanujan's thinking style. Here is one comment which he gave: I have often been asked whether Ramanujan had any special secret; whether his methods differed in kind from those of other mathematicians; whether there was anything really abnormal in his mode of thought. I cannot answer these questions with any confidence or conviction; but I do not believe it. My belief is that all mathematicians think, at bottom, in the same kind of way, and that Ramanujan was no exception .5

Here Hardy states in essence his own version of the Church-Turing Thesis. I paraphrase: CHURCH-TURING THESIS, HARDY'S VERSION: At bottom, all mathematicians are isomorphic.

This does not equate the mathematical potential of mathematicians with that of general recursive functions; for that, however, all you need is to show that some mathematician's mental capacity is no more general than recursive functions. Then, if you believe Hardy's Version, you know it for all mathematicians.

Then Hardy compares Ramanujan with calculating prodigies:

His memory, and his powers of calculation, were very unusual, but they could not reasonably be called "abnormal". If he had to multiply two large numbers, he multiplied them in the ordinary way; he could do it with unusual rapidity and accuracy, but not more rapidly and accurately than any mathematician who is naturally quick and has the habit of computations

Hardy describes what he perceived as Ramanujan's outstanding intellectual attributes: With his memory, his patience, and his power of calculation, he combined a
power
of generalisation, a feeling for form, and a capacity for rapid modification of his
hypotheses
, that were often really startling, and made him, in his own field, without a rival in his day.'

The part of this passage which I have italicized seems to me to be an excellent characterization of some of the subtlest features of intelligence in general. Finally, Hardy concludes somewhat nostalgically:

[His work has not the simplicity and inevitableness of the very greatest work; it would be greater if it were less strange. One gift it has which no one can deny-profound and invincible originality. He would probably have been a greater mathematician if he had been caught and tamed a little in his youth; he would have discovered more that was new, and that, no doubt, of greater importance. On the other hand he would have been less of a Ramanujan, and more of a European professor and the loss might have been greater than the gain.8

The esteem in which Hardy held Ramanujan is revealed by the romantic way in which he speaks of him.

"Idiots 'Savants"

There is another class of people whose mathematical abilities seem to defy rational explanation-the so-called "idiots savants", who can perform complex calculations at lightning speeds in their heads (or wherever they do it). Johann Martin Zacharias Dase, who lived from 1824 to 1861 and was employed by various European governments to perform computations, is an outstanding example. He not only could multiply two numbers each of 100 digits in his head; he also had an uncanny sense of quantity. That is, he could just "tell", without counting, how many sheep were in a field, or words in a sentence, and so forth, up to about 30-this in contrast to most of us, who have such a sense up to about 6, with reliability. Incidentally, Dase was not an idiot.

I shall not describe the many fascinating documented cases of "lightning calculators", for that is not my purpose here. But I do feel it is important to dispel the idea that they do it by some mysterious, unanalyzable method. Although it is often the case that such wizards' calculational abilities far exceed their abilities to explain their results, every once in a while, a person with other intellectual gifts comes along who also has this spectacular ability with numbers. From such people's introspection, as well as from extensive research by psychologists, it has been ascertained that nothing occult takes place during the performances of lightning calculators, but simply that their minds race through intermediate steps with the kind of self-confidence that a natural athlete has in executing a complicated motion quickly and gracefully. They do not reach their answers by some sort of instantaneous flash of enlightenment (though subjectively it may feel that way to some of them), but-like the rest of us-by sequential calculation, which is to say, by FlooP-ing (or BlooP-ing) along. -

Incidentally, one of the most obvious clues that no "hot line to God" is involved is the mere fact that when the numbers involved get bigger, the answers are slower in coming. Presumably, if God or an "oracle" were supplying the answers, he wouldn't have to slow up when the numbers got bigger. One could probably make a nice plot showing how the time taken by a lightning calculator varies with the sizes of the numbers involved, and the operations involved, and from it deduce some features of the algorithms employed.

The Isomorphism Version of the Church-Turing Thesis

This finally brings us to a strengthened standard version of the Church-Turing Thesis: CHURCH-TURING THESIS, ISOMORPHISM VERSION: Suppose there is a method which a sentient being follows in order to sort numbers into two classes.

Suppose further that this method always yields an answer within a finite amount of time, and that it always gives the same answer for a given number. Then: Some terminating FlooP program (i.e.,