Financial Markets Operations Management (52 page)
Read Financial Markets Operations Management Online
Authors: Keith Dickinson

At the moment a buyer and seller agree to a transaction, both parties have a contingent liability to do something:
- The buyer is committed to pay cash (in exchange for the purchased securities);
- The seller is committed to deliver securities (in exchange for the sale proceeds).
The accounting entries should reflect these commitments at the earliest possible opportunity (ideally on the trade date). Transactions are not usually settled on the trade date; most are
settled at a later date in accordance with market convention for the product being settled. Due to these timing differences, these entries will have to be split into two stages:
- Trade date â to reflect the commitment.
- Settlement date â to discharge the commitment.
The entries are passed using the appropriate general ledger accounts using a system of double-entry bookkeeping.
As we saw above, on the trade date the company takes the liability onto its books. Let us look at an example where the company purchases securities costing USD 10,000. Using the “T-account” format, the accounting entries for this purchase would be posted as shown in
Table 13.3
.
TABLE 13.3
Accounting entries (a)
| Details | Dr | Â | Details | Cr |
| Securities at cost | USD 10,000 | Â | Cash | USD 10,000 |
There are two problems with this posting:
- It assumes that the cash has, in fact, been paid. Even for same-day settlement, there will be a timing difference between the actual trade execution and the actual payment of cash.
- The posting does not reflect the counterparty's part in this transaction. Until such time as the transaction settles, the counterparty is the company's creditor.
A better way would be to post the trade date entries as shown in
Table 13.4
.
TABLE 13.4
Accounting entries (b)
| Details | Dr | Â | Details | Cr |
| Securities at cost | USD 10,000.00 | Â | Creditors (counterparty) | USD 10,000.00 |
If the securities were equities and the transaction included brokerage fees of, say, USD 100.00, then the entries would be posted as shown in
Table 13.5
.
TABLE 13.5
Accounting entries (c)
| Details | Dr | Â | Details | Cr |
| Securities at cost | USD 10,000.00 | Â | Creditors (counterparty) | USD 10,100.00 |
| Brokerage | USD Â Â Â Â 100.00 | Â | Â | Â |
| Total: | USD 10,100.00 | Â | Total: | USD 10,100.00 |
Let us change the transaction to a bond purchase with a nominal amount of USD 100,000 and a price of 101.2500. Interest has accrued at 4% p.a. for 65 days (30E/360). Convention has it that the securities at cost should be calculated at the clean price and any accrued interest added separately, as shown in
Table 13.6
.
TABLE 13.6
Accounting entries (d)
| Details | Dr | Â | Details | Cr |
| Securities at cost | USD 101,250.00 | Â | Creditors (counterparty) | USD 101,972.22 |
| Accrued interest | USD Â Â Â Â Â Â 722.22 | Â | Â | Â |
| Total: | USD 101,972.22 | Â | Total: | USD 101,972.22 |
Finally, if this same bond is sold some days later at a clean price of 101.50 plus 75 days' accrued interest, the entries would be posted as shown in
Table 13.7
.
TABLE 13.7
Accounting entries (e)
| Details | Dr | Â | Details | Cr |
| Debtors (counterparty) | USD 102,333.33 | Â | Securities at cost | USD 101,500.00 |
| Â | Â | Â | Accrued interest | USD Â Â Â Â Â Â 833.33 |
| Total: | USD 102,333.33 | Â | Total: | USD 102,333.33 |
Entries across the securities at cost ledger would be sub-divided into one of the several asset/liability accounts and reflected on the Balance Sheet.
On settlement of a transaction, the cash is paid or received and entries posted to contra the creditor/debtor account and credit/debit the cash (bank) account. The net result would be (a) above, i.e. the purchase of securities has been debited to Securities at cost and credited to Cash. The Creditor account has been cleared by the two compensating entries.
We revalue a particular security or a portfolio of securities to establish how much they are worth. The true valuation of any security can only occur when you dispose of a long position (or cover a short position). Otherwise you can only have an estimate of that value, even though the price that you obtain can be regarded as being accurate.
| (b) Settlement of securities purchase | ||||
| Details | Dr | Â | Details | Cr |
| Creditors (Counterparty) | USD 10,000.00 | Â | Cash | USD 10,000.00 |
| (c) Settlement of equities purchase | ||||
| Details | Dr | Â | Details | Cr |
| Creditors (Counterparty) | USD 10,100.00 | Â | Cash | USD 10,100.00 |
| (d) Settlement of bond purchase | ||||
| Details | Dr | Â | Details | Cr |
| Creditors (Counterparty) | USD 101,972.22 | Â | Cash | USD 101,972.22 |
| (e) Settlement of bond sale | ||||
| Details | Dr | Â | Details | Cr |
| Cash | USD 101,500.00 | Â | Debtors (Counterparty) | USD 101,500.00 |
FIGURE 13.3
Settlement entries
For example, you may have purchased 100 shares at a price of JPY 1,000 per share and wish to revalue them. The price on the Tokyo Stock Exchange is JPY 1,200 per share and shows a potential profit of JPY 200 per share. You decide that now is the time to take your profit and sell the shares. You go into the market and find that its best bid price is JPY 180 per share. If you then decide to execute the transaction you will certainly have made a profit, but not as much as you had first thought.
So, taking any price for a revaluation is, at best, only ever going to be an indicative figure. The situation can become more complicated in the OTC markets, where a price may not be readily available. In this situation, you might need to get opinions from several market participants, who may have, at some stage, been buyers or sellers, or make use of an appropriate mathematical model that would calculate a price.
The topic of revaluation becomes more important in the mutual fund industry where the price of a fund is calculated from the net asset value (NAV) of the fund. To do this, the fund manager must calculate the value of each of the underlying securities in the fund, less any liabilities.
1
Any errors in pricing will cause the NAV to be inaccurate and the subsequent price of shares in the fund will be either understated or overstated. The consequences of incorrect pricing will almost certainly lead to a loss for the fund manager, mainly as a result of refunding cash to sellers or giving extra shares to purchasers.
This type of revaluation is commonly known as
mark-to-market
(MTM), and is performed on a daily basis with the results being fed through to the Profit & Loss account.
Securities are always quoted with a bid price and an offer price. As an investor, which of these two prices would you use to revalue your portfolio of, say, equities? If you are not sure of the answer, think about your portfolio from the point of view of its disposal. What price would you get if you were to sell the shares? You would get the market's bid price (the market is bidding to buy from you as a seller). By contrast, if your portfolio contains short positions, what price would you get if you had to cover the short? You would get the market's offer price (the market is offering to sell to you as a buyer).
Our portfolio of Singaporean equities showed an overall gain of SGD 3,600, with the share prices of DBS, Global Logistic and Jardine Cycle all increasing. These are theoretical gains only, as we would not benefit from them unless we sold the shares. We therefore refer to these gains as
unrealised gains
. Notice that the share prices for Charisma and Singapore Airlines decreased â we would show these losses as
unrealised losses
.
Our basic accounting approach depends on the type of investment that we have made (see
Table 13.9
).
TABLE 13.9
Type of investment
| Type of Investment | Basic Accounting Approach | Assessment Guidelines |
| Trading | Fair value (mark-to-market) with gains/losses posted to Operating Income | We intend to buy and sell for short-term profits |
| Held-to-maturity | Amortised cost | We intend to buy and hold until a fixed maturity date |
| Available-for-sale | Fair value with gains/losses posted to Other Comprehensive Income | Default category; similar to Trading except in the manner in which gains and losses are treated |
If we mark-to-market our assets on a daily basis, we account for any gains and losses at the same time; in other words, we drip-feed gains and losses throughout the period in which we are holding the assets. By contrast, if we value at historic cost, then the assets are valued at the original purchase/sale price and only show the total gain or total loss on the eventual sale of the long position (or purchase to cover a short position).
Let us take one of these securities and follow the daily MTM revaluation process, as shown in
Table 13.10
.
TABLE 13.10
Revaluation process
| Jardine Cycle & Carriage Ltd, Shares (C07) | Trading Book | |
| Date | Details | Price |
| Â 7 April 2014 | You purchase 6,000 shares | SGD 36.77 |
| Â 7 April 2014 | Closing price | SGD 35.65 |
| Â 8 April 2014 | Closing price | SGD 36.16 |
| Â 9 April 2014 | Closing price | SGD 35.00 |
| 10 April 2014 | Closing price | SGD 34.06 |
| 11 April 2014 | Closing price | SGD 34.21 |
| 14 April 2014 | You sell 3,500 shares | SGD 34.78 |
| 14 April 2014 | Closing price | SGD 34.42 |
We can observe that 6,000 shares were purchased at SGD 36.77. The loss on the sale of 3,500 shares was SGD 1.99 per share (SGD 34.78 â SGD 36.77) totalling SGD 6,965 (3,500 shares at a loss of SGD 1.99 per share).
By concentrating on the 3,500 shares sold, marking the position to market every day and accounting for any gains and losses on a daily basis, we can see in
Figure 13.4
the way in which the loss was spread over the seven days.
| Â | Â | Number | Â | Â | Gain/ | Â |
| Date | Details | Shares | Price | Amount | Loss | Balance |
| Â 7 Apr 2014 | Purchase | 3,500 | SGD 36.77 | SGD (128,695) | Cost | SGD (128,695) |
| Â 7 Apr 2014 | Closing price | 3,500 | SGD 35.65 | SGD Â Â Â Â 3,920 | Loss | SGD (124,775) |
| Â 8 Apr 2014 | Closing price | 3,500 | SGD 36.16 | SGD Â Â Â (1,785) | Gain | SGD (126,560) |
| Â 9 Apr 2014 | Closing price | 3,500 | SGD 35.00 | SGD Â Â Â Â 4,060 | Loss | SGD (122,500) |
| 10 Apr 2014 | Closing price | 3,500 | SGD 34.06 | SGD Â Â Â Â 3,290 | Loss | SGD (119,210) |
| 11 Apr 2014 | Closing price | 3,500 | SGD 34.21 | SGD Â Â Â Â Â (525) | Gain | SGD (119,735) |
| 14 Apr 2014 | Sale | 3,500 | SGD 34.78 | SGD 121,730 | Proceeds | SGD Â Â Â Â Â Â 1,995 |
| Â | Â | Â | Â | Unrealised Gain/ Loss - B/Dwn | Â | SGD Â Â Â (8,960) |
| Â | Â | Â | Â | Â | Â | Â |
| Â | Â | Â | Â | Realised Gain/ Loss on Sale | Â | SGD (6,965) |
Notes:
(1) Although the original purchase was for 6,000 Jardine Cycle & Carriage Ltd shares, we are focusing on the quantity that was sold on 14 April.
(2) The result of the daily MTM calculations resulted in an unrealised loss of SGD 8,960 (refer to the tinted fields in the Amount and Balance columns of the figure).
(3) The sale on 14 April showed a gain of SGD 1,995; that was because the sale price of SGD 34.78 was compared with the closing price on the previous business day (11 April) of SGD 34.21.
(4) Overall, therefore, the realised loss was the sum of the unrealised loss plus the gain on the sale date.
(5) If we re-combine the original purchase, the sale and the balance of these shares, we have a final position of 2,500 shares valued at SGD 86,050, as shown in
Figure 13.5
.
FIGURE 13.4
Sale of 3,500 Jardine Cycle & Carriage shares
The clean price of a bond depends on several factors such as:
- The creditworthiness of the issuer;
- The remaining time to maturity of the bond;
- The overall market conditions including the yield.
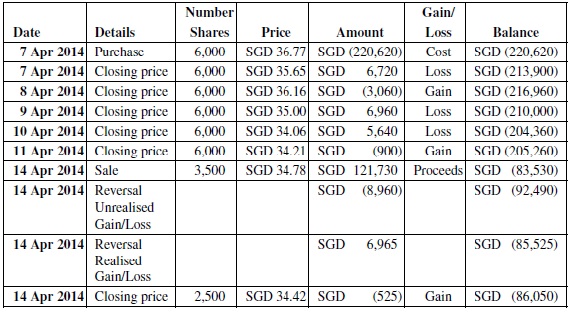
FIGURE 13.5
Final position of Jardine Cycle & Carriage shares
We wish to purchase a bond, issued by ABC, with a coupon rate of 3% p.a. (paid annually) and with exactly ten years to maturity. We can calculate the clean price, all things being equal, using an appropriate yield. In
Table 13.11
we can see, for a selection of yields, the clean prices of this bond would be:
TABLE 13.11
Bond prices using yields
| ABC 3% Bonds due for Maturity in 10 Years | |||
| Face Value | Yield | Price | Price is at: |
| 100,000 | 2.0000% | 108.9826 | A premium to par |
| 100,000 | 3.0000% | 100.0000 | Par |
| 100,000 | 4.0000% | Â Â 91.8891 | A discount to par |
Note:
Prices calculated using the bond function of a Texas Instruments BAII Plus calculator.
As we are holding this bond to maturity and the bond matures at par, we can identify two features:
- The issuer will only pay the cash proceeds from the bond on maturity of the bond (i.e. in ten years' time in our example).
- Buying the bond at a premium will result in a loss (and at a discount, a gain).
Having checked your answers, please note that:
- If you purchased the bond at a price above par, you would only receive par on maturity, i.e. you would lose 8,982.60.
- Conversely, if you purchased the bond at a price below par, you would still receive par on maturity, i.e. you would gain 8,110.90.
- There would be neither a gain nor a loss if you had purchased the bond at par.
For scenarios 1 and 2 above, the gain/loss would be amortised over the remaining life of the bond (i.e. ten years in our example) rather than as one amount on the maturity of the bond. The term
amortise
can therefore be described as: “an amount drip-fed (or ârecognised') in the financial accounts over the life of the bond”.
The following spreadsheets illustrate the cash treatment for the amortisation.
As there is neither a gain nor a loss, we only need to account for the purchase cost, regular coupon payments (3,000.00 p.a.) and redemption proceeds (100,000.00) â see
Figure 13.6
.
| Date | Cash Received | Â | Coupon Income | Â | Investment in ABC Bonds |
| Today | â100,000.00 | CR | Â | Â | 100,000.00 |
| Year 1 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 2 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 3 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 4 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 5 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 6 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 7 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 8 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 9 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 10 | 3,000.00 | DR | Â 3,000.00 | CR | Â |
| Year 10 | 100,000.00 | DR | Â | Â | â100,000.00 |
| Â | 30,000.00 | = | 30,000.00 | Â | Â Â Â Â Â Â Â Â 0.00 |
FIGURE 13.6
Bonds purchased at par
The loss of 8,982.60 will be amortised over the ten-year period and will be recognised as a reduction of the coupon income. In this example, the loss will be 898.26 p.a. and will be deducted from the annual coupon of 3,000.00. This premium/loss will be recognised over the life of the bond as a decrease in interest income â see
Figure 13.7
.
| Â | Cash | Â | Coupon | Â | Premium | Â | Investment in |
| Date | Received | Â | Income | Â | Amortisation | Â | ABC Bonds |
| Today | â108,982.60 | CR | Â | Â | Â | Â | 108,982.60 |
| Year 1 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 108,084.34 |
| Year 2 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 107,186.08 |
| Year 3 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 106,287.82 |
| Year 4 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 105,389.56 |
| Year 5 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 104,491.30 |
| Year 6 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 103,593.04 |
| Year 7 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 102,694.78 |
| Year 8 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 101,796.52 |
| Year 9 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 100,898.26 |
| Year 10 | 3,000.00 | DR | 2,101.74 | CR | 898.26 | CR | 100,000.00 |
| Year 10 | 100,000.00 | DR | 0.00 | Â | 0.00 | Â | 0.00 |
| Â | 21,017.40 | = | 21,017.40 | Â | 8,982.60 | Â | Â |
FIGURE 13.7
Bonds purchased at a premium
This will be similar to the premium treatment, only in reverse. The gain will be amortised at 811.09 plus the annual coupon of 3,000.00. This discount/gain will be recognised over the life of the bond as an increase in interest income â see
Figure 13.8
.
| Â | Cash | Â | Coupon | Â | Discount | Â | Investment in |
| Date | Received | Â | Income | Â | Amortisation | Â | ABC Bonds |
| Today | â91,889.10 | CR | Â | Â | Â | Â | Â 91,889.10 |
| Year 1 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 92,700.19 |
| Year 2 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 93,511.28 |
| Year 3 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 94,322.37 |
| Year 4 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 95,133.46 |
| Year 5 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 95,944.55 |
| Year 6 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 96,755.64 |
| Year 7 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 97,566.73 |
| Year 8 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 98,377.82 |
| Year 9 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | Â 99,188.91 |
| Year 10 | 3,000.00 | DR | 3,811.09 | CR | 811.09 | DR | 100,000.00 |
| Year 10 | 100,000.00 | DR | 0.00 | Â | 0.00 | Â | â0.00 |
| Â | 38,110.90 | = | 38,110.90 | Â | 8,110.90 | Â | Â |
FIGURE 13.8
Bonds purchased at a discount