Coming of Age in the Milky Way (3 page)

Consequently the idea slowly took hold that an adequate model of the universe not only should be internally consistent, like a song or a poem, but should also make accurate predictions that could be tested against the data of observation. The ascendency of this thesis marked the beginning of the end of our cosmological childhood. Like other rites of passage into adulthood, however, the effort to construct an accurate model of the universe was a bittersweet endeavor that called for hard work and uncertainty and deferred gratification, and its devotees initially were few.

One was Eudoxus. He enters the pages of history on a summer day in about 385
B.C
., when he got off the boat from his home town of Cnidus in Asia Minor, left his meager baggage in cheap lodgings near the docks, and walked five miles down the dusty road to Plato’s Academy in the northwestern suburbs of Athens. The Academy was a beautiful spot, set in a sacred stand of olive trees, the original “groves of academe,” near Colonus, blind Oedipus’ sanctuary, where the leaves of the white poplars turned shimmering silver in the wind and the nightingales sang day and night. Plato’s mentor Socrates had favored the groves of academe, which even Aristophanes the slanderer of Socrates described lovingly as “all fragrant with woodbine and peaceful content.”
⁶

Beauty itself was the principal subject of study at the Academy, albeit beauty of a more abstract sort,
LET NONE BUT GEOMETERS ENTER HERE
, read the motto inscribed above the door, and great was the general enchantment with the elegance of geometrical forms. Geometry (
geo-metry
, “earth-measurement”) had begun as a practical affair, the method employed by the Egyptian rope-stretchers in the annual surveys by which they reestablished the boundaries of farmlands flooded by the Nile. But in the hands of Plato and his pupils, geometry had been elevated to the status approaching that of a theology. For Plato, abstract geometrical forms
were
the universe, and physical objects but their imperfect shadows. As he was more interested in perfection than imperfection, Plato wrote encomiums to the stars but seldom went out at night to study them.

He backed this view with an imposing personal authority. Plato was not only smart, but rich—an aristocrat, one of the “guardians”
of Greek society, descended on his mother’s side from Solon the lawmaker and on his father’s from the first kings of Athens—and physically impressive;
Plato
, meaning “broad-shouldered,” was a nickname bestowed upon him by his gymnastics coach when as a youth he wrestled in the Isthmian Games. Eudoxus, we may assume, was suitably impressed. He was, however, a geometer in his own right—he was to help lay the foundations of Euclidean geometry and to define the “golden rectangle,” an elegant proportion that turns up everywhere from the Parthenon to the paintings of Mondrian—and, unlike Plato, he combined his abstract mathematical reasonings with a passion for the physical facts. When he made his way to Egypt (a pilgrimage to the seat of geometrical wisdom that many Greek thinkers undertook, though Plato seems never to have got around to it), Eudoxus not only conducted research in geometry but applied it to the stars, building an astronomical observatory on the banks of the Nile and there mapping the sky. The observatory, though primitive, evinced his conviction that a theory of the universe must answer to the verdict, not only of timeless contemplation, but of the ceaselessly moving sky.

When the mature Eudoxus returned to the Academy, now as a renowned scholar with his own retinue of students, he set to work crafting a model of the cosmos that was meant to be both Platonically pleasing and empirically defensible. It envisioned the universe as composed of concentric spheres surrounding the earth, itself a sphere.
^*
This in itself would have gratified Plato, who esteemed the sphere as “the most perfect” of the geometric solids, in that it has the minimum possible surface area relative to the volume of space it encloses. But the Eudoxian universe was also intended to better fit the observed phenomena, and this aspiration mandated complexity. To the simple, spherical cosmos that had been proposed by Parmenides a century earlier, Eudoxus added more spheres. The new spheres dragged and tugged at those of the sun, moon and planets, altering their paths and velocities, and by adjusting their rates of rotation and the inclination of their axes Eudoxus found that he could, more or less, account for retrograde motion and other intricacies of celestial motion. It took a total of twenty-seven
spheres to do the job. This was more than Plato would have preferred, but it answered somewhat more closely to the data than had the preceding models. The hegemony of pure, abstract beauty had begun its slow retreat before the sullen but insistent onslaught of the material world.

But, ultimately, even so complex a cosmos as that of Eudoxus proved inadequate. The data base kept improving—with the conquest of Babylon by Alexander the Great in 330
B.C
., the Greeks gained access to such Babylonian astronomical records as had previously eluded them, while continuing to make at least intermittent observations of their own—and Eudoxus’ model failed to explain the subtleties revealed by this more ample and refined information. Thus began the phoenixlike cycle of the
science
of cosmology, where theories, however grand, are held hostage to empirical data that has the power to ruin them.

The next round fell, for better or worse, to Aristotle. Routinely described in the textbooks as an empiricist alternative to Plato, Aristotle was, indeed, relatively devoted to observation; he is said, for instance, to have spent his honeymoon collecting specimens of marine life. But he was also addicted to explanation and intolerant of ambiguity, qualities not salutary in science. A physician’s son, he inherited a doctor’s bedside habit of having a confident and reassuring answer to every anxious question. When pressed, this cast of mind made him credulous (women, he asserted, have fewer teeth than men) and propelled him to the extremities of empty categorizing, as when he observed that “animals are to be divided into three parts, one that by which food is taken in, one that by which excrement is discharged, and the third the region intermediate between them.”
⁷
Aristotle wrote and lectured on logic, rhetoric, poetry, ethics, economics, politics, physics, metaphysics, natural history, anatomy, physiology, and the weather, and his thinking on many of these subjects was subtle as dewfall, but he was not a man to whose lips sprang readily the phrase, “I do not know.” His mind was a killing jar; everything that he touched he both illuminated and anesthetized.

Nobody really likes a man who knows everything, and Aristotle became the first known victim of the world’s first academic politics. Though he was an alumnus of the Academy and its most celebrated teacher, and clearly the man best qualified to succeed Plato as its director, he was twice passed over for the post. He then
took the only satisfactory course open to a man of his stature, and stalked off to teach at another institution. As there
was
no other academic institution, he was obliged to found one; such was the origin of the Lyceum.

When it came time for Aristotle to declaim on the structure of the universe, he based his model on the heavenly spheres of Eudoxus, whom he had esteemed at the Academy for his moderate character as well as for his peerless accomplishments in astronomy. As his research assistant on the cosmology project Aristotle chose the astronomer Callippus, a native of Eudoxus’ adopted home of Cyzicus. Together Aristotle and Callippus produced a model—consistent, symmetrical, expansive, and graceful to contemplate—that ranks among the most stirring of history’s many errant cosmologies. Enshrined in Aristotle’s book
De Caelo (On the Heavens)
, it was to beguile and mislead the world for centuries to come.

Its details need not detain us; they consisted principally of adding spheres and adjusting their parameters, with the result that the universe now sported fully fifty-five glistening, translucent spheres. Beyond its outermost sphere, Aristotle argued on exquisite epistemological grounds, nothing could exist, not even space. At its center sat an immobile Earth, the model’s shining diadem and its fatal flaw.

Confronted with an inevitable disparity between theory and observation, cosmologists who worked from the geocentric hypothesis had little choice but to keep making their models ever more complicated. And so cosmology was led into a maze of epicycles and eccentrics in which it would remain trapped for over a thousand years. The virtuoso of this exploration was Claudius Ptolemy.

He was born in the second century
A.D
. in Ptolemais on the Nile, and funding for his astronomical studies came from the Ptolemaic dynasty via the museum of Alexandria. Whatever his shortcomings—and many have been exposed, including evidence that he laundered some of his data—he was a hardworking astronomer and no armchair theorist. He charted the stars from an observatory at Canopus, a city named for a star, situated fifteen miles east of Alexandria, and was acquainted with atmospheric refraction and extinction and many of the other tribulations that bedevil the careful observer. He titled his principal cosmological work
Mathematical Syntaxis
, meaning “the mathematical composition,” but it
has come down to us
Almagest
, Arabic for “the greatest.” What it did so splendidly was predict the motions of the sun, moon, and stars more accurately than had its predecessors.

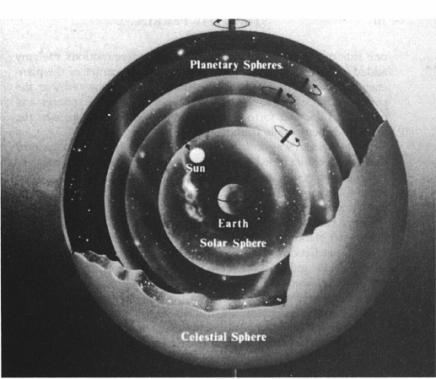
Aristotle’s universe consisted of spheres nested within spheres, their axes and directions of rotation adjusted to approximate the observed motions of the sun, moon, and stars across the sky. (Not to scale.)

The epicycles and eccentrics by which Ptolemy sought to reconcile theory and observation had been introduced by the geometer Apollonius of Perga and refined by the astronomer Hipparchus. Epicycles were little circular orbits imposed upon the orbits of the planets: If a planet for Aristotle circled the earth like an elephant on a tether, the same planet for Ptolemy described the path of a stone whirled on a string by the elephant’s rider. Eccentrics further improved the fit between the inky page and the night sky, by moving the presumptive center of the various heavenly spheres to
one side of the center of the universe. To these motions Ptolemy added another, circular motion pursued by the center of the planetary spheres: The elephant’s tether pole itself now orbited the center of the universe, hauling the whole system of spheres and epicycles back and forth so that planets could first approach the earth and then recede from it.

The system was ungainly—it had lost nearly all the symmetry that had commended celestial spheres to the aesthetics of Aristotle—but it worked, more or less. Wheeling and whirring in Rube Goldberg fashion, the Ptolemaic universe could be tuned to predict almost any observed planetary motion—and when it failed, Ptolemy fudged the data to make it fit. In its elaboration, and in the greater elaborations that later astronomers were obliged to add, it made predictions accurate enough to maintain its reputation as “the greatest” guide to heavenly motion from Ptolemy’s day down to the Renaissance.

The price Ptolemy’s followers paid for such precision as his model acquired was to forsake the claim that it represented physical reality. The Ptolemaic system came to be regarded, not as a mechanical model of the universe, but as a useful mathematical fiction. All those wheels within wheels were not actually out there in space—any more than, say, the geometrical boundary lines recorded in the Alexandrian land office represented real lines drawn across the silted farmland along the Nile. As the fifth-century Neoplatonist Proclus noted, “These circles exist only in thought…. They account for natural movements by means of things which have no existence in nature.”
⁸
Ptolemy himself took the position that the complexities of the model simply reflected those found in the sky; if the solution was inelegant, he noted, so was the problem:

The aim of the theory, then, was not to depict the actual machinery of the universe, but merely to “save the appearances.” Much fun has been made of this outlook, and much of it at Ptolemy’s expense, but science today has frequent recourse to intangible abstractions
of its own. The “spacetime continuum” depicted by the general theory of relativity is such a concept, and so is the quantum number called “isospin,” yet both have been highly successful in predicting and accounting for events in the observed world. It should be said in Ptolemy’s defense that he at least had the courage to admit to the limitations of his theory.