Bully for Brontosaurus (50 page)
Read Bully for Brontosaurus Online
Authors: Stephen Jay Gould

WHY DO WE CARE
so much about size and number? My friend Ralph Keyes, who tips the charts with me at five feet seven and a half inches, wrote an entire book about our obsession with this supposedly irrelevant subject
—The Height of Your Life
. He documented the extraordinary steps that short politicians and film stars often take to avoid discovery of their secret. (Ralph couldn’t penetrate the subterfuges of Jimmy Carter’s staff to discover the height of our shortest recent president, who is at least an inch or two taller than Ralph and me, and therefore at, or not far from, the American average.) The most amusing item in Ralph’s book is an old publicity shot of a short Humphrey Bogart with two of his leading ladies, Lauren Bacall and Katharine Hepburn. They have just emerged from an airplane. Bogie is on the first step of the gangplank; the two women stand on the ground.
Why do we so stupidly equate more with better? Penises and automobiles, two objects frequently graded for size by foolish men, work just as well, and often more efficiently, at smaller than average lengths. Extremes in body size almost always entail tragic consequences (at least off the basketball court). Robert Wadlow, just shy of nine feet and the tallest human ever recorded, died at age twenty-two from infection caused by a faulty ankle brace needed for supplementary support since his legs could not adequately carry his body. Moving beyond the pathology of extreme individuals, entire species of unusually large body size generally have short geological lifetimes. I doubt that their problem lies in biomechanical inefficiency, as earlier theories of lumbering dinosaurs held. Rather, large creatures tend to be anatomically specialized and form relatively small populations (fewer brontosauruses than boll weevils)—perhaps the two strongest detriments to extended survival in a world of large and capricious environmental fluctuation over time.
While most people do understand that large size does not guarantee long-term success, the myth of “more is better” still pervades our interpretations. I have, for example, noted with surprise, as I have monitored the impressions of students and correspondents for more than twenty years, how many people assume, as almost logically necessary a priori, that evolutionary “progress” and complexity should correlate with the amount of DNA in an organism’s cell—the ultimate baseline for more is better. Not so. The very simplest creatures, including viruses at the low end, followed by bacteria and other prokaryotic organisms, do have relatively little DNA. But as soon as we reach multicellular life, based on eukaryotic cells with nuclei and chromosomes, the correlation breaks down completely. Mammals stand squarely in the middle of the pack, with 10
9
–10
10
nucleotides per haploid cell. The largest values, ranging to nearly 100 times more DNA than the most richly endowed mammals, belong to salamanders and to some flowering plants.
Many species of plants arise by polyploidy, or doubling of chromosome number. These doublings often run through several cycles among a group of closely related species, so the amount of DNA can increase greatly—and the high DNA content of some polyploid plants has never been much of a mystery. On the other hand, the extreme values for amphibians once puzzled zoologists sufficiently that they gave the phenomenon a name—“the C-value paradox.” However, since the discovery that so little of the total DNA codes actively for enzymes and proteins, this hundredfold difference between some mammals and salamanders seems less troubling. Most DNA consists of repeated copies; much of it codes for nothing and may represent “junk” in terms of an organism’s morphology. The hundredfold difference does not mean that salamanders have 100 times more active genes than mammals, for the disparity occurs chiefly in nonessential, or noncoding, regions. (We would still, of course, like to know why some groups accumulate more junk and more repetitions, but such differences do not merit special recognition as a formal paradox.)
This essay considers another expression of maximum and minimum, and another test of correlation between quantity and quality—numbers of chromosomes. We have voluminous data on average differences in number of chromosomes among groups of organisms, and some patterns surely emerge. Diptera (flies and their allies) tend to have few per cell;
Drosophila
, the great laboratory stalwart (and largely for this reason), harbors four pairs per diploid cell. Birds tend to have many. Instead of providing a compendium for these well-chronicled differences, I shall focus on the extreme cases of more and less among organisms. Extreme values may titillate our fancy, but they are also unusually instructive for recognizing and specifying generalities. Exceptions do prove rules. (The etymology of that cliché, usually mistaken for a reversed meaning, is not “prove” in the sense of verify, but “probe” in the sense of test or challenge. This definition, from the Latin
probare
, is not entirely archaic in English—consider printer’s proof, or a proving ground for testing weapons.)
Until two years ago, the lowest number of chromosomes, a commandingly minimal one pair, had been found for only a single organism—a nematode worm, appropriately honored in its subspecific name as
Parascaris equorum univalens
. This minimal complement had been discovered long ago, in 1887, by Theodor Boveri, the greatest cytologist (student of cellular architecture) of the late nineteenth century. Boveri (1862–1915) was a great intellectual in the European tradition—a complex and fascinating man who lived for the laboratory, but who also played the piano and painted with professional competence. His short life was scarred by fits of depression, and he died in despondency as the First World War enveloped Europe. Of Boveri’s many scientific discoveries, the two greatest centered on chromosomes. First, he established their individuality and shifted attention from the nucleus as a whole to chromosomes as the agent of inheritance (in years before the rediscovery of Mendel’s laws). Second, he demonstrated the differential value of chromosomes. Before Boveri’s experiments, many scientists had conjectured that each chromosome carried all the hereditary information, and that organisms with many chromosomes carried more copies of this totality. Boveri proved that each chromosome carried only part of the hereditary information (some of the genes, as we might say today), and that the full complement built the organism through a complex orchestration of development.
Boveri took great interest in his discovery of an organism that carried but one pair of chromosomes per cell—and therefore did place all its hereditary information into one package. But Boveri quickly discovered that
P. equorum univalens
, though no imposter in its claims to minimalism, was not entirely consistent either. Only the cells of the germ line, those destined to produce eggs and sperm by meiosis, kept all the hereditary material together in a single pair of chromosomes. In cells destined to form body tissues, this chromosome fractured several times during the first cleavage divisions of early embryology, leading to adult cells with up to seventy chromosomes!
Finally, in 1986, Australian zoologists Michael W. J. Crosland and Ross H. Crozier reported a remarkable new species within a closely related group of ants, previously united into the overextended species
Myrmecia pilosula
(see their article of 1988 cited in the bibliography). This name falsely amalgamates several distinct species sharing a similar body form, but carrying different numbers of chromosomes in their cells. Species with nine, ten, sixteen, twenty-four, thirty, thirty-one, and thirty-two pairs of chromosomes have been described. Obviously, this complex of forms has evolved some way of speciating in concert with substantial changes in chromosome number.
On February 24, 1985, on the Tidbinbilla Nature Reserve near Canberra, Crosland and Crozier collected a colony of winged males and females, plus a mated queen with pupae and more than 100 workers. All workers tested from this colony carried but a single pair of chromosomes in their cells—all of them, not just cells of a particular type. An unambiguous example of chromosomal minimalism had finally been discovered, almost exactly 100 years after Boveri found only one pair of chromosomes in the germ line cells of
Parascaris
.
But the story of
M. pilosula
is even better, deliciously so. If you were out searching for absolute minimalism, you would have to root for finding your single pair of chromosomes in an ant, bee, or wasp—for the following interesting reason: The Hymenoptera, and just a few other creatures, reproduce by an unusual genetic system called haplodiploidy. In most animals, all body cells contain chromosomes in pairs, and sex is determined by maternal and paternal contributions (or noncontributions in some cases) to a single pair. But haplodiploid organisms specify sex by a different route. Reproductive females usually store sperm, often for long periods. Genetic females (including the functionally neuter workers) arise from fertilized eggs, and therefore contain chromosomes in pairs. But males are produced when the queen fails to fertilize a developing egg with stored sperm (in most other animal groups unfertilized eggs are inviable). Thus, the cells of male ants, bees, and wasps do not carry chromosomes in pairs and bear only the single set inherited from their mother. These males have no father, and their cells contain only half the chromosomes of females—a condition called haploid, as opposed to the diploid, or paired, complement of their sisters. (The entire system therefore receives the name haplodiploid, or male-female in this case.)
Haplodiploidy implies, of course, that males of the Tidbinbilla colony of
M. pilosula
have a truly and absolutely minimal number of one chromosome per cell. Not even a single pair—just one. The only lower possibility is disappearance. Crosland and Crozier checked just to be sure. The males of their colony contained a single chromosome per cell.
If we have reached a limit in the search for less, the other extreme seems more open-ended. How many chromosomes can a cell contain and still undergo the orderly divisions of mitosis and meiosis? Can hundreds of chromosomes line up neatly along a mitotic spindle and divide precisely to place an equal complement into each daughter cell? At what point do things become so crowded that this most elegant of biological mechanisms breaks down?
Maximal numbers are most easily reached by polyploidy, or doubling of chromosomes. This process occurs in two basic modes with differing evolutionary significances. In autoploidy, a cell doubles its own complement, forming, initially at least, a cell with two sets of identical pairs. Thus, the new autoploid usually looks like its parent. Autoploidy is not a mechanism for rapid evolution of form, though the redundancy introduced by doubling does permit considerable evolutionary divergence afterward—as one member of the duplicated pair becomes free to change. On the other hand, alloploidy, the second mode of doubling, can produce viable hybrids between distant species and can serve as a mechanism for sudden and substantial changes in form. Hybrids, with different forms and numbers of maternal and paternal chromosomes, will usually be sterile because chromosomes have no partners for pairing before meiosis—the “reduction division” that produces sex cells with half the genetic information of body cells. But if the precursors of sex cells undergo polyploidy, then each chromosome will find a partner in the duplicated version of its own form.
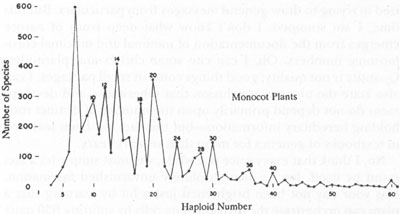
Since polyploidy is so much more common in plants than animals, we should search for maximalism in our gardens, not our zoos. The numerical importance of polyploidy in plants can best be appreciated in a wonderful graph that I first encountered, when a graduate student, in Verne Grant’s
The Origin of Adaptations
. This graph is a frequency distribution for chromosome pairs in monocot plants. For ten pairs of chromosomes and higher, without exception, all peaks are for even numbers of chromosome pairs.
At first inadequate sight, this pattern doesn’t make sense in the deepest possible way. Biology is not numerology; its regularities do not take the form of such abstractions as “cleave to even numbers.” Such a graph will not be satisfying until we figure out a biological mechanism that, as a side consequence and not because evens are better than odds per se, produces an imbalance of species with chromosomes in pairs of even numbers. The resolution is elegantly simple in this case. Polyploidy is very common in plants, and every number, odd or even, when doubled, yields an even number. The peaks therefore indicate the prevalence of polyploidy in plants. Estimates range as high as 50 percent for the number of angiosperm species produced by polyploidy.
Since polyploidy can continue in cycles—doubling followed by redoubling—chromosome numbers, like the pot in a poker game with table stakes, can rise alarmingly from small beginnings. The champions among all organisms are ferns in the family Ophioglossaceae. The genus
Ophioglossum
exhibits a basic number of 120 chromosome pairs, the lowest value among living species. (Such a high number must, itself, be derived from earlier incidents of polyploidy among species now extinct. The basic number for the entire family, 15 pairs, may have been the starting point.) In any case, cycles of polyploidy have proceeded onward from this already large beginning of 120 pairs. The all-time champion, not only in
Ophioglossum
, but among all organisms, is
Ophioglossum reticulatum
, with about 630 pairs of chromosomes, or 1,260 per cell! (The total need not be an exact multiple of 120, because doubling may be imperfect, and secondary gains or losses for individual chromosomes are common.)