Birth of a Theorem: A Mathematical Adventure (29 page)

Even if a homogeneous solid is heated in a very uneven manner, so that at any given instant the temperature varies abruptly and erratically from one place to another, the solid has only to be allowed to cool for a fraction of a second for the temperature distribution to smooth out, that is, to vary in a regular manner. This phenomenon, known as parabolic regularization, is one of the first things students learn about in an introductory course on partial differential equations. The corresponding mathematical statement enjoys an importance that goes well beyond the field of physics.

If the solid is inhomogeneous, however, being composed of various materials, at each position x it will have a more or less great conductivity C
(
x
)
, which is to say a more or less great capacity for cooling. As a result, the equation changes:

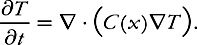
Does the property of regularization still hold true in this context?

Nash, unlike Nirenberg, had no special expertise in PDEs. Just the same, he took the bait. Week after week he kept coming back to discuss the problem with Nirenberg—and to pick his brains.

At first Nash’s questions were naïve, questions a beginner might ask. Nirenberg started to wonder whether Nash really deserved his reputation. It takes courage, when you are already famous and admired, to act the novice in a field you haven’t yet mastered—courage, or else a quite unusual degree of self-confidence! The willingness to risk the embarrassment of appearing less than brilliant in the hope that the answer to an unexpected query will point you in the right direction. But this is the price of making progress on a difficult problem.… Little by little Nash’s questions became more precise, more pertinent. An idea was beginning to form in his mind.

Later, back at MIT, Nash continued to work on the problem. Always the same modus operandi: prying information out of one colleague, asking advice from another, explaining the obstacles he had encountered to someone else.

Lennart Carleson, a very talented Swedish analyst, spoke to him about Boltzmann and entropy. Carleson was one of the few mathematicians at the time who was well versed in the subject—not quite by accident, as it happens, since he was Torsten Carleman’s literary executor. Carleman was the first mathematician to really tackle Boltzmann’s equation in earnest. At the time of his death he had left an unfinished manuscript on the topic, and it was Carleson’s job to complete it and see it through publication. This is how Carleson became familiar with the notion of entropy, and why he was able to help Nash.

But Boltzmann and Fourier aren’t at all the same thing—entropy and regularity have nothing to do with each other!

Somehow a light went on in Nash’s brain. A plan of attack began to take shape. Without showing his cards, the young mathematician continued to make his rounds, knocking on doors, picking up a lemma here, a proposition there.

John Nash

Finally, one morning, the reality of the situation was obvious to all: by combining all the contributions of his various collaborators with unsurpassable skill, Nash had proved the theorem—like an orchestra conductor, or a film director, who gets each player to play his part of the score, or the script, just perfectly.

At the heart of the proof was entropy. Under Nash’s direction, entropy was cast against type to tremendous effect. His manner of using differential inequalities involving certain quantities, inspired by an interpretation that was half mathematical, half physical, founded a new style of analysis, and with it a tradition that I am proud to carry on in my own way.

THIRTY

Princeton

May 4, 2009

My neck touches the carpet—and instantly a wave of well-being radiates throughout my body, from my head to my toes. Back to my office after lunch, 1:00 p.m., maybe a bit later: just the right moment for a bit of relaxation.

Not the violent kind of relaxation that the astrophysicists in the building next door are so excited about, but not a gentle one either. The only soft thing between me and the floor of my modest office is a thin-pile carpet. Still, you can feel the carpet against your neck, and once you get used to it you wouldn’t want it to be any thicker than it is.

Images pass before my closed eyes, one after the other, sounds chirping in my ears, louder and louder. The whole morning replays itself in my head.…

*   *   *

A class from the Littlebrook Elementary School came to visit the Institute today. The pond, the magnificent trees in blossom, the great bust of Albert Einstein in the old library—look, kids, the magic castle of science! Eight years old isn’t too young to be dreaming about great scientists.

I’d prepared a twenty-minute talk. I told them about Brownian motion, which reveals the world of atoms; and then explained the famous Syracuse problem, which is so simple that a child of eight can understand it—and so complex that the best mathematician in the world throws up his hands in despair.

They listened attentively, staring in wonder at the marvelous images of Brownian movement roaming across the screen of my laptop, which I held up for all to see. In the last row, a wide-eyed fair-haired little boy listened still more attentively than the others. He had been living here only four months, and yet he had no trouble understanding what his father was saying in English with a French accent so thick you could cut it with a knife.

Then the rest of the morning, then another good lunch, then—and then my brain began to fog over, as it often does this time of day. Time to make a fresh start, a clean break—a reboot, as I call it. You restart the computer, clearing its memory and beginning all over again.…

*   *   *

Ears ringing, the children chattering away, everything spinning around. Facial muscles relax; the ringing more intense now, sentence fragments flapping about, some more loudly than others; voices and songs, the meal once more, a forgotten spoon, a formal welcome, an unfrozen lake, a bust in my library, 3
n
+
1, 3
n
+
2, 3
n
+
3, the parquet and the shadows and you forgot a small child and …

A sudden slight tremor in my limbs, the mists disperse. My mind is clear once more.

I remain still for another moment, stretched out on the floor. Some ants are scurrying across the soles of my feet.…

My feet have disappeared from my internal radar. Incredibly heavy, impossible to move. Like when a clump of snow gets stuck to the bottom of your ski and you can’t lift it up.

And yet on my first try, as if by magic, movement is restored to my feet, and once again I am whole. The break is over, ten minutes exactly. I’m a new mathematician.

Cedric reboot (completed)

A new Cédric. Time to embark on a fresh round of calculations. There’s also an article on Landau damping, more than fifty years old but still very relevant today, that I just got from the library. Now for two hours of intense concentration before tea …

*   *   *

The Syracuse problem (also known as the Collatz conjecture or the
3
n
+
1 problem
) is one of the most famous unsolved enigmas of all time. Paul Erd
ő
s himself is on record as saying that mathematics is not yet ready to confront such monsters.

Enter the expression
“3
n
+
1”
in an Internet search engine and follow the thread back to the abominable problem and its result, as simple and insistent as the refrain of a pop song:

Take any whole number you like, say
38.

This number is even. Divide it by
2
and you get
19.

This last number is odd. Multiplying by
3
and adding
1
you get
19
×
3
+
1
=
58.

This last number is even. Divide it by
2.…

And so on. You go on from one number to the next by means of a simple rule: each time you encounter an even number, divide by
2
; each time you encounter an odd number, multiply by
3
and add
1.

Starting
from
38
,
as in the example above,
you get the following sequence:
19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1 …

Once you arrive at
1
,
in other words, you know what comes next:
4, 2, 1, 4, 2, 1, 4, 2, 1…, ad calculam aeternam.

Every single time this calculation has been performed in the course of human history, it has ended up at
4, 2, 1.…
Does that mean it will
always
turn out thus, no matter which number is chosen as the point of departure?

Since there are infinitely many integers, obviously it’s impossible to try all of them. With all the pocket calculators, desktop calculators, computers, and supercomputers at our disposal today, it has nevertheless been possible to try billions and billions of them, and every last one has wound up leading back to the implacably repeating
4, 2, 1
pattern.

Mathematics is democratic, of course, and anyone is free to try to show that this sequence embodies a general rule. Everyone believes the rule to be true, but since no one knows how to prove it, it remains a conjecture. Whoever succeeds in confirming or disconfirming this conjecture will be proclaimed a hero.

I am certainly not among those who will try. Apart from the fact that it seems to be phenomenally difficult, it isn’t the sort of problem that suits the way my mind works. My brain isn’t used to thinking about such things.

*   *   *

Date: Mon, 4 May 2009 17:25:09
+
0200

From: Cedric Villani

To: Clement Mouhot

Subject: Backus

So here’s Backus’s article from JMP 1960 (Vol.1 No.3, too bad it wasn’t Vol.1 No.1!)

Fantastic! Take a look at the next-to-last section of Backus’s article, and then the last sentence of the article. It’s all the more remarkable since as far as I’m aware no one has explicitly expressed these doubts until recently, the last few years …

Best

Cedric

Date: Sun, 10 May 2009 05:21:28
+
0800

From: Clement Mouhot