Birth of a Theorem: A Mathematical Adventure (13 page)

“Are you all right? Really, there’s no point worrying yourself sick! Relax, take it easy.”

“Can’t.”

“You really seem obsessed.”

“Look, I’m on a mission. It’s called nonlinear Landau damping.”

“I thought you were supposed to be working on the Boltzmann equation. That was your big project, wasn’t it? You don’t want to lose sight of what you came here to do, do you?”

“Can’t be helped. Right now it’s Landau damping.”

But Landau damping goes on playing the cold, unattainable beauty. I can’t get next to her.

… Still, there’s that little calculation I did on getting home from the museum—doesn’t that give some reason for hope? But man, is it ever complicated! I added two more parameters to the norm. Our norms used to have five regularity indices, which already was the world record—now they’re going to have seven! But so what, applying the two indices to a function that doesn’t depend on velocity leaves you with the same norm as before, there’s no inconsistency.… I’ve got to check the calculation carefully. But if I try to do it right now, it’s going to turn out wrong, so let’s wait until tomorrow! I’m going to have to do the whole damn thing over again, this time with norms that have got seven indices. Good Lord.

Seeing how glum I looked, Claire felt sorry for me. Or at least felt she had to do something to cheer me up.

“Look, tomorrow’s Sunday. You can spend the day at the office if you like; I’ll take care of the little lambkins.”

At that moment, nothing in the world could have pleased me more.

*   *   *

Date: Sun, 18 Jan 2009 10:28:01 -0500

From: Cedric Villani

To: Clement Mouhot

Subject: Re: transfer

On 01/18/09, 13:12, Clement Mouhot wrote:

>
“Any news on your end?”

I’m making progress … two steps forward and one step back to begin with, but after a while I became convinced that if we keep going about it your way we won’t gain enough in large time. I’ve found another method that gives us more just on the time variable, it seems to work well enough except for one thing: it involves somewhat more complicated spaces, with an additional 2 indices:-) However all the estimates seem to come out the same for this new family, still we’ll have to check very carefully to be sure. In any case these are supersubtle tricks, and I think one of the hearts of the problem. This evening I’ll send you a new version if all goes well, with a few holes yet to be filled in, and we should be able to begin working in parallel once more.

Best

Cedric

Date: Sun, 18 Jan 2009 17:28:12 -0500

From: Cedric Villani

To: Clement Mouhot

Subject: Re: transfer

Here’s the revised file. For it all to hold together (I haven’t mentioned Newton’s scheme yet), we’ll have to (i) check to see that the “bihybrid” norms I’ve introduced at the end of section 4 exhibit the same properties as the “simple” hybrid norms, and that therefore one gets similar estimates for the characteristics in these norms(!); (ii) find a way of combining the two distinct effects that are described in the new section 5; (iii) put all that at the end of chapter 7 and fill in the missing details to give an estimate for the total density; (iv) check everything! In other words, our plates are full. For the moment I suggest that you go over what I’ve written and tell me if you see anything that doesn’t look right. I’ll let you know later if I see things that we can clearly work on together at the same time …

A few more points:

I think your estimates for transfer of regularity were flawed, the result was too strong, I wasn’t able to reproduce them in the usual norms; on the other hand I did use your transfer strategy in section 5. But when you try to apply it in large time (t\to\infty, \tau remaining small) the transfer seems to crash, the permissible exponents don’t allow the integral to converge over time. I concocted (don’t ask me how) a method for getting more integration over time, but this time without getting more regularity. We’ve got to find a way to combine the two.

More later, best

Cedric

Date: Mon, 19 Jan 2009 00:50:44 -0500

From: Cedric Villani

To: Clement Mouhot

Subject: Re: transfer

I’ve gone through the file again and cleaned it up a bit, so the attached version should be considered definitive. Going forward I suggest the following division of labor:

– you see to it that Proposition 4.17 and Theorem 6.3 are in good shape, that’s asking a lot, I know, but it will have the advantage of forcing you to go over my estimates in sections 4 and 6 again line by line:-) which has to be done, because if we make a mistake calculating the conditions that the exponents must satisfy we’re sunk. For the moment in both these sections I’ve entered some pretty much arbitrary statements as placeholders, with guesstimates that for all I know may turn out to be right but it may also turn out that reality is more complicated. No need to recheck the proofs, but we do have to be absolutely sure about the bounds we end up with, everything else depends on them.

– in the meantime I’ll get to work finishing sections 5 and 7 (modulo the input that will come from Theorem 6.3).

– also I’m going to talk to Tremaine tomorrow about the physics part of the intro.

– if you have time to flesh out your comment following, you can incorporate it in the introduction to section 5, where I’ve already mentioned the connection with averaging lemmas. (Be careful, since we’re working in the analytic class it’s not wholly obvious that this is an L^1/L^\infty phenomenon??)

If you can get started right away, and assuming all goes well, it ought to be possible to get all this done 2-3 days from now, and only Newton/Nash–Moser will be left to work out in detail. (But I think our priority has to be getting the statements in 4.17 and 6.3 right so we’re sure we’re not building castles in the air.)

Best

Cedric

Date: Mon, 19 Jan 2009 13:42:27
+
0100

From: Clement Mouhot

To: Cedric Villani

Subject: Re: transfer

Hi Cedric,

it’s turning into a real monster;)!!

*   *   *

Excerpts from aggregate file-3 (January 18, 2009)

4.7 Bihybrid norms

We shall be led to use the following more complicated norms:

Definition 4.15.
We define the space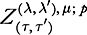
by

(…)

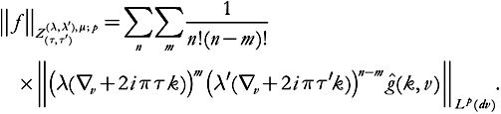
After trial and error, the best we could do was to recover this decay in the “bihybrid” norms described in subsection 4.7:

Proposition 5.6 (regularity-to-decay estimate in hybrid spaces).

Let
f
=
f
_t
(
x, v
)
, g
=
g
_t
(
x, v
)
,
and

Then

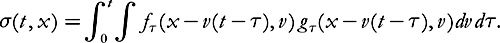
THIRTEEN

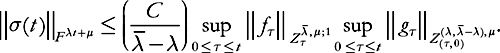
Princeton

January 21, 2009

Thanks to the rabbit I pulled out of my hat on my returning from the museum the other evening, I’ve been able to get back on track. But today I’m filled with a strange mixture of optimism and dread. Got around one major roadblock: made a few explicit calculations and eventually figured out how to manage a term that had gotten too big—that much gives me hope. At the same time, the complexity of the mathematical landscape that’s now opened up makes my head spin if I think about it for more than a few moments.

Could it really be that Vlasov’s splendid equation, which I thought I was beginning to get a handle on, operates only by fits and starts? On paper, at least, it looks as though sometimes the response to external perturbations suddenly occurs very, very quickly. I’ve never heard of such a thing; it’s not in any of the articles and books that I’ve read. But in any case we’re making progress.

*   *   *