Alan Turing: The Enigma (107 page)

Alan had much developed his friendship with the writer Nick Furbank – a development which perhaps reflected his greater willingness to branch away from science, and even to interest himself in literature. The subject of suicide had entered at some point in their conversation, and Nick recalled it when he wrote
⁴⁰
to Robin on 13 June, describing what he had found at Wilmslow, when he went there in his capacity of executor. But this had lent no sense of explanation to the death, only perhaps the knowledge that it was not a course that Alan had ruled out of court. Nor did Franz Greenbaum, despite close acquaintance with Alan’s inner life and dreams, feel that anything was understood. The dream books were recovered and passed back to the psychoanalyst, but did not answer any questions.

John Turing read through two of the dream books, which Franz Greenbaum lent to him before destroying them. Alan’s ‘scarifying’ comments on his mother, and his description of homosexual activity since adolescence, told John far more than he ever wished to know, and he found these revelations in themselves sufficient explanation for what had occurred, thankful only that he had managed to prevent them from reaching his mother’s eyes. To Alan’s friends, nothing could be so clear.

There was one piece of evidence that he had prepared for death: he had made a new will on 11 February 1954. This in itself was a kind of statement as to where he stood. It made Nick Furbank his executor, rather than his brother, and gave to Robin all his mathematical books and papers. Then after £50 legacies to each member of his brother’s family, and £30 to his housekeeper, the remainder was divided between his mother, Nick Furbank, Robin Gandy, David Champernowne and Neville Johnson. John Turing was amazed and appalled at Alan having thus lumped his mother together with his friends – but this very fact was a much warmer gesture to her than a more conventional allocation which treated her not as an individual friend but as a person to whom he owed a family duty.
^*

Yet the will included a provision that his housekeeper should have a further £10 for each year in which she had been employed after the end of 1953 – a strange point to add if he had then been settled upon death. It seemed to Nick, on visiting the scene, that Alan had arranged certain letters into packets – but there was no wholesale clearing up, neither of personal papers nor of his research. It was as though he had planned for the possibility, but in the event acted impulsively. What factors were there, at a less immediate level, that might have prompted such plans?

He died on a Whit Monday, the coldest and
wettest Whit Monday for fifty years, as it happened. Was it, symbolically, the day
after
inspiration, when the spirit was beginning to give out? G.H. Hardy had attempted suicide in 1946, although in his case, as one who had gone seven years deprived of creative life by a stroke. Was there an underlying pattern in Alan Turing’s life and death on this second layer of the psychological onion? The self-revelation of his ‘short story’ would suggest that he thought of himself as having had his ‘inspiration’ in 1935, and it being thereafter a fight to maintain that level. And the waves of inspiration had come only once every five years since Christopher Morcom’s death: the Turing machine in 1935, naval Enigma in 1940, the ACE in 1945, the morphogenetic principle in 1950. At least, these were the outward expressions of his thought; he worked rather like the Turing machine that he arranged to write and do rough working on alternate squares. There had been a good deal of
reculer pour mieux sauter
in between.

In each case he had become not exactly bored or disillusioned by the last flood of work, but felt he had exhausted what he could achieve within its framework. He was, as compared with a more conventional academic, peculiarly anxious not to be enclosed or defined by his existing reputation. So indeed by 1954 or 1955 he would need something new to emerge, to maintain his freshness. But by June 1954 it was hardly time for despair. Indeed, the 1949 period had probably been much more difficult for him.

Possibly the morphogenetic work had turned out rather plodding and laborious. It was three years since he had claimed he could account for the fir cone pattern, and he had not achieved it when he died. But there was no sign of a dropping off of interest. In the summer of 1953 he had taken on a research student, Bernard Richards. (There had been an earlier student, who had achieved nothing.) Richards took over some detailed calculations in connection with his models for the formation of patterns on spherical surfaces. He worked out some exact solutions to Alan’s equations, thus exhibiting the capacity of the theory to accommodate some of the simpler possible patterns found in the monocellular
Radiolaria
. Alan had a book of engravings
^*
of these oceanic organisms, which he would show with delight to the engineers when on his night shift.

The working relationship had not progressed beyond the master-and-servant kind, but even so, it was clear to Richards that there was no decline or fall in Alan’s work, not even at the very end. He was doing a good deal of writing up, but this was not at the expense of new experimentation on the computer. Nor, in any case, was this a very dramatic kind of theory, which stood to be proved right or wrong in an all or nothing way. It was a stage on which he could play out ideas in chemistry and geometry and see where they led. It was open-ended, and depended upon integrating insights into many different branches of mathematics and science, rather than trying to solve a particular problem within a given framework.

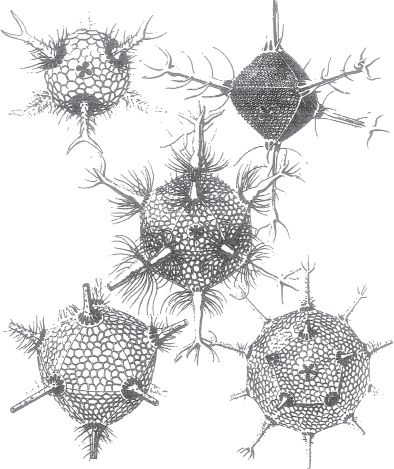
Part of a plate from Ernst Haeckei’s report on
Radiolana
.

He left behind a mass of detailed material,
⁴¹
some organised into the form of a second paper, the rest in the form of worked examples and of computer print-outs incomprehensible to anyone else. Typical of his investigations at the time of his death was the following passage:

The amplitude of the waves is
largely controlled by the concentration V of ‘poison’.

In his
Natural Wonders
way, he called the chemical whose function was to
inhibit
growth, the ‘poison’ – a macabre touch, given that in his own body it had recently been the other way round. He continued:

If the quantity R is small it means that the poison diffuses very fast. This reduces its power of control, for if the U values are large in a patch and large quantities are produced, the effect of the poison will mainly be to diffuse out of the patch and prevent the increase of U in the neighbourhood. … If R is allowed to be
too large
it can happen that the ‘side-band suppression’ effect even prevents the formation of a hexagonal lattice. …

Such observations reflected an insight gained from many trials even with this one model which was, as it happened, an ‘Outline of Development of the Daisy’. He had quite literally been ‘watching the daisies grow’ – not only by ‘examining 15 plants’, rather as he had done with Joan Clarke in 1941, but on his universal machine. But this was only one particular branch of his investigations: there was another headed FIRCONES, with an associated computer routine OUTERFIR; and another headed KJELL theory, which concerned another form of his basic equations, and which was associated with routines called KJELLPLUS, IBSEN and other Nordic names. All of this went rather beyond the material that he was writing up for publication, so there was no lack of prospects.

He was working with Robin on the theory of types, and they planned to write a joint paper. He also wrote a popular article on the ‘word problem’, which appeared in the Penguin
Science News
in early 1954.
^*
The Russian
mathematician P.S. Novikov had announced
⁴²
that the ‘word problem’ for groups was indeed unsolvable by any definite method; Alan’s article explained this and tied it in with some questions in topology, showing that the problem of deciding whether some knot was the same as some other knot was essentially a ‘word problem’ of this kind. It was up to date, and looked forward to the complete proof of the Russian result becoming available. He was interested in solving problems up to the end: a last letter of May 1954 to Robin discussed certain ideas of Robin’s for ‘getting round the Gödel argument’ but ended with: ‘Looked at the rainbow problem again. Can do it rather successfully for sound, but total failure for electricity. Love, Alan.’ When out walking together in Charnwood Forest, near Leicester, they had seen an unusual double rainbow, a phenomenon that Alan insisted on analysing. There had to be a reason for it.

If he was looking for something new, it was in theoretical physics, which likewise he had put on one side since the 1930s. Before the war he had spoken to Alister Watson of his interest in the ‘spinors’ that appeared in Dirac’s theory of the electron, and in his last year he did some work
⁴³
on the algebraic foundations of the spinor calculus. He defined what he called ‘founts’, after printers’ founts of type.
^*
He was also interested in the idea Dirac had suggested in 1937,
⁴⁴
according to which the constant of gravitation would change with the age of the universe. Once at lunchtime he said to Tony Brooker, ‘Do you think that a
palaeontologist
could tell from the
footprint
of an extinct
animal
, whether its weight was what it was
supposed
to be?’ And always distrustful of the official line in quantum mechanics, he revived his interest in the foundations of the subject. He found a paradox within the standard interpretation, as von Neumann had set it out, because he noticed that if a quantum system were ‘observed’ frequently enough, its evolution could be made indefinitely slow, and in the limit of continuous observation would freeze to a stop. Thus the standard account depended upon an implicit assumption that this mysterious moment of ‘observation’ occurred only at discrete intervals.

He had some further heretical ideas which he explained to Robin:
⁴⁵
‘Quantum Mechanists always seem to require infinitely many dimensions; I don’t think I can cope with so many – I’m going to have about a hundred or so – that ought to be enough, don’t you think?’ And he had the germ of another idea: ‘Description must be non-linear, prediction must be linear.’ A shift of interest on his part into fundamental physics would have been well-timed;
the development of relativity theory was to begin a great revival in 1955, after years in wartime doldrums. The interpretation of quantum mechanics, little developed since von Neumann’s work in 1932, was also a subject crying out for new ideas, and was one well suited to his particular kind of mind.

It was not true, as Mrs Turing liked to think, that he was on the verge of making an ‘epoch-making discovery’ when he died; on the other hand, there was no clear pattern of decline or failure in his intellectual life that might in itself explain its abrupt end. It was rather a fluid, transitional period such as had occurred before in his development, and this time accompanied by a wider range of interests, and a more open attitude to intellectual and emotional life.

Nor, as others saw it, was this last year in any way eventful; quite the reverse. One strange incident alone stood out, and might have pointed to the existence of matters on his mind that few could possibly appreciate. It was in mid-May 1954, when Alan went with the Greenbaum family for a Sunday visit to Blackpool. It was a very fine day, and they walked cheerfully along the Golden Mile of seaside amusements, until they came across the Gypsy Queen, the fortune-teller. Alan went in, to consult her. Had not a gypsy foretold his genius, in 1922? The Greenbaums waited outside, and found themselves waiting for half an hour. When he came out, he was as white as a sheet, and would not speak another word as they went back to Manchester on the bus. They did not hear from him again, until he called on the Saturday two days before his death when, as it happened, they were out. They heard of his death before returning the call.

What was his fortune?
Audentes Fortuna Juvat
was the Turing family motto, but his uncle Arthur had died in the Great Game, ambushed in an ill-protected British position in 1899. As for Alan, in the great Looking Glass game of life, it was less clear what happened. But there was certainly a part of his mind which Robin and Nick and Franz Greenbaum did not know, and which did not belong to himself, but to those who moved the pieces: White and Red. The board was ready for an end game different from that of Lewis Carroll’s, in which Alice captured the Red Queen, and awoke from nightmare. In real life, the Red Queen had escaped to feasting and fun in Moscow. The White Queen would be saved, and Alan Turing sacrificed.