World's 200 Hardest Brain Teasers (11 page)
Read World's 200 Hardest Brain Teasers Online
Authors: Dr. Gary R. Gruber

125. (c) 3 vs. 3
Label the 9 coins
a, b, c, d, e, f, g, h, i.
First weigh
abc
with ghi. If they balance, then heavy coin is
d, e,
or
f.
So weigh
d
with e. If they balance, then the heavy coin is f. If they don’t balance, then whichever coin tips the scale is the heavy one. Suppose
abc
and
ghi
do not balance. Then whichever side tips the scale has the heavier coin. Suppose in this case the side with
ghi
has the heavy coin. Then, in the procedure done before, weigh
g
with
h.
If they balance, then
i
is heavy. If they don’t balance, then the coin that tips the scale downward is heavy.
Here is a more sophisticated solution:
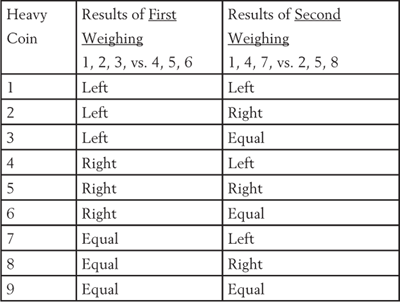
Number the coins 1 through 9. In the first weighing, place coins 1, 2, and 3 on the left side of the scale, and place 4, 5, and 6 on the right side. Leave 7, 8 and 9 on the side. For the second weighing, regardless of the results of the first, place coins 1, 4, and 7 on the left, and place 2, 5, and 8 on the right. The following chart demonstrates how to determine which is the heaviest coin depending on these results. In this chart, the results displayed list which side of the balance scale was heavier.
126. He or she should open the remaining door.
The probability would be 2/3, not 1/2! Many people have thought that there is a 1/2 chance of having the car behind the door the contestant chose since there are two doors. However, because you have chosen a door first, out of three, there is a 1/3 probability there is a car behind it, and there would be a 2/3 probability any other door has the car behind it. So if you chose two of the other doors, you would have a 2/3 probability of the car. And if one door was eliminated by the host, since that door had the goat, if you switched doors, then it would be in effect as if you were choosing two doors, which would give you the 2/3 probability that the car was behind the remaining door.
Another explanation:
Interestingly enough, the answer is that the contestant should switch doors, because there is actually a 2/3 chance of winning the car by switching, while there is only a 1/3 chance of winning the car if the contestant opens his or her original door!
This is how most people’s minds approach the problem: The host eliminates one door with the goat, so there is a goat or a car behind the contestant’s door. So the probability is 1/2. And it doesn’t matter whether the contestant opens his or her original door or changes doors. But let’s see what is really happening. The probability of having a car behind the contestant’s door when he or she originally chooses the door is 1/3, since there are three doors and only one door that has a car behind it. And there is a 2/3 probability that the car is behind one of the other two doors (since there are two ways a car can be behind one of the remaining doors [car-goat; goat-car] out of a total of three possibilities: car-goat; goat-car; goat-goat). Now, if the host eliminates a door, there would still be the 1/3 probability that the car was behind the contestant’s original door—so once a door is eliminated, there is a 2/3 probability the car was behind the remaining door.
I have pondered the
Let’s Make a Deal
problem for some time, and I came to the conclusion that it is 2/3 when I took a more dramatic variation of the problem. Suppose I had 100 doors and 1 of them had a car behind it. The rest had goats. If I chose one door, there would no doubt be a 1/100 chance that there was a car behind it. So the remaining doors combined would have a 99/100 chance of the car. Now no matter what was done to the other doors, there would still be a 1/100 chance of the car’s being behind the door that was chosen. So if the host knew that 98 of the doors did not have the car, and then eliminated those doors, the remaining door then must have had a 99/100 chance that there was a car behind it.
Suppose you had 100 doors. The chance of the car’s being behind the contestant’s chosen door is 1/100, obviously a very slim chance that won’t change even when the host eliminates 98 doors. When the doors are eliminated, and all but two are left, the contestant still has chosen a door with a very, very slim chance the car is behind it, namely 1/100. Because the host knows where the car is (and where the goats are), and because 98 of the goats were eliminated, the remaining door has a (98 + 1)/100 chance there is a car behind it.
Note that initial reasoning may indicate that when there is only one door left, since 98 doors have been eliminated, the total number of possibilities for what’s behind the contestant’s door is two, a car or a goat. The favorable number of possibilities is one, the car. So by strict definition of probability, the probability is 1/2 no matter what the host knows or did. But according to the previous paragraph, that is not the case.
I think probability has a somewhat ambiguous definition, especially if there is “conditional” probability, but it seems that if you tried the 100 doors out you would in fact find you’d get a 1/100 chance of getting the car.
127. X = w; Y = h; and Z = t: where there were.
128. 43
Call
x
the number of boxes with 6 donuts,
y
the number of boxes with 9 donuts, and
z
the number of boxes with 20 donuts. Then the total number of donuts,
N
, for
x
,
y
,
z
boxes is represented by
N
= 6
x
+ 9
y
+ 20
z
, or
N
= 3(2
x
+ 3
y
) + 20
z
. Now
x
= 0, 1, 2, 3 etc.,
y
= 0, 1, 2, 3, etc.,
z
= 0, 1, 2, 3, etc.
20z can be 20, 40, 60, etc.
3(2x + 3y) can be 0, 6, 9, 12, 15, 18, 21, 24, 27, and any multiple of 3 thereafter.
So all the combinations become: 0, 6, 9, 12, 15, 18, 21, 24, 26, 27, 29, 30, 32, 33, 35, 36, 38, 39, 40, 41, 42, 44 (which is 20 + 24), 45, 46 (which is 40 + 6), 47 (which is 20 + 27), 48, 49 (which is 40 + 9), 50 (which is 20 + 30), 51, etc., and all consecutive numbers thereafter. The greatest number that you cannot make is 43.
129. 2/7
Cross out all the common numerators and denominators. That is, cross out, the 3s, 4s, 5s and 6s. We are left with 2/7. Note that this is a problem that could be done faster
without
a calculator!
130. (d) pygmy : undersized
Suppose you don’t know the meaning of the word MENDACIOUS. Mendacious is an adjective probably describing a LIAR. So assume that a LIAR has the characteristic of being mendacious. A pygmy has the characteristic of being undersized. Note that an artist may not be creative.
131. (b) m
Write the sequence as follows: a l b (c, d) e m f (g, h) i n j (k, l). So the next letter is m.
132. 1/3
The favorable outcomes (of spelling an English word) are two: NOT and TON.
The total number of ways of arranging the three letters in a row is six: NTO, NOT, TON, TNO, OTN, ONT. Thus the probability is 2/6 = 1/3.
133. 4,950
This is extremely tricky. Write the numbers as:
1 + 2 + 3 + 4 +…+ 99 =
N
and then write the numbers below that in reverse:
99 + 98 + 97 + 96 +…+ 1 =
N
Adding both sums we get 100 + 100 + 100…(99 times)
This is just 99 x 100, which is just 2
N
.
So
N
= 50 x 99 = 99 x 100/2 = 4,950
134. 4,951
Look at the first numbers in the parts of the sequence:
First = 1
Second = 2
Third = 4
Fourth = 7
Fifth = 11
Note the first number of the parts of the sequence increase by 1, 2, 3, 4, etc.
(If you add 1 to the first number, you get the second. If you add 2 to the second number, you get the third. If you add 3 to the third number, you get the fourth. If you add 4 to the fourth number, you get the fifth.)
So, the first number, call it
N
in the
nth
part of the sequence is
1:
N
= 1 + [1 + 2 + 3 + … + (
n
- 1)]
Now write this again backwards:
2:
N
= 1 + [(
n
- 1) + (
n
- 2) + (
n
- 3) + … + 1] + 1
Adding (1) and (2), we get 2
N
= 1 + [(1 +
n
- 1) + (2 +
n
- 2) + (3 +
n
- 3) + … + (
n
- 1 + 1)].
This is just equal to 2
N
= 1 + 1 + [
n
taken (
n
- 1) times], or just 2 +
n
(
n
- 1).
So
N
= [2 +
n
(
n
- 1)]/2. So, if
n
= 100, then
N
= [2 + 100(99)]/2 = [2 + 9,900]/2 = 4,951
135. 70°

Make isosceles triangles: Where R is on AC, draw BR = BC; where Q is on AB, draw RQ = RB. Where M is on AC, draw MQ = RQ. We have BAC = 20°,
BAC = 20°, ABC = 80°,
ABC = 80°, ACB = 80°.
ACB = 80°.
You can find that:
 BRC = 80°,
BRC = 80°, RBC = 20°,
RBC = 20°, QBR = 60°,
QBR = 60°, RQB = 60°,
RQB = 60°, QRB = 60°,
QRB = 60°, QRM = 40°,
QRM = 40°, QMR = 40°, and
QMR = 40°, and MQR = 100°.
MQR = 100°.