Warped Passages (43 page)

The Large Hadron Collider will explore this energy range. If supersymmetry is not discovered at the LHC, which will search for particles up to a few thousand GeV in mass, it will mean that superpartners are too heavy to solve the hierarchy problem, and the supersymmetry solution will be ruled out.

But if supersymmetry solves the hierarchy problem, it will be an experimental windfall. A particle accelerator that explores energies of about a TeV (1,000 GeV) will find, in addition to the Higgs particle, a host of supersymmetric partners of Standard Model particles. We should see gluinos and squarks, as well as sleptons, winos (pronounced “weenos,” not like Bowery bums), a zino, and a photino. The new particles would have all the same charges as Standard Model particles, but would be heavier. With sufficient energy and collisions, these particles would be hard to miss. If supersymmetry is right, we will soon see it confirmed.

Supersymmetry: Weighing the Evidence

This leaves us with the outstanding question: does supersymmetry exist in nature? Well, the jury is still out. Without more facts, any answer is mere conjecture. At the moment both the defense and the prosecution have compelling arguments in their favor.

We have already mentioned two of the strongest reasons to believe in supersymmetry: the hierarchy problem and the superstring. A third compelling piece of evidence in favor of supersymmetry is the potential unification of forces in supersymmetric extensions of the Standard Model. As discussed in Chapter 11, the interaction strengths of the electromagnetic, weak, and strong forces depend on energy. Although Georgi and Glashow originally found that the Standard Model forces unify, better measurements of these three forces showed that unification in the Standard Model doesn’t quite work. A plot of the three interaction strengths as a function of energy is presented in the upper graph in Figure 66.

However, supersymmetry introduces many new particles that interact via these three forces. This changes the distance (or energy) dependence of the forces because supersymmetric partners also appear as virtual particles. These additional quantum contributions enter the renormalization group calculation and influence how the interaction strengths of the electromagnetic, weak, and strong forces depend on energy.

The lower graph in Figure 66 shows how the strengths of the forces depend on energy when the effect of virtual superpartners is included. Remarkably, with supersymmetry the three forces appear to unify more precisely than ever. This is more significant than the earlier unification attempts because we now have much better measurements of the interaction strengths. The intersection of three lines could be coincidence. But it might also be taken as evidence in support of supersymmetry.

Another nice feature of supersymmetric theories is that they contain a natural candidate for dark matter. Dark matter is the nonluminous matter that pervades the universe and has been discovered through its gravitational influence. Even though about one-quarter of the energy
in the universe is stored in dark matter, we still don’t know what it is.
^*
A supersymmetric particle that does not decay and has the right mass and interaction strength would be a suitable dark matter candidate. And indeed, the lightest supersymmetric particle doesn’t decay, and could have the right mass and the right interactions to be the particle of which dark matter is composed. This lightest superpartner could be the photino, the partner of the photon. Or, in the extra-dimensional scenario that we’ll consider later on, it could be the wino, the partner of the W gauge boson.

However, the case for supersymmetry is not airtight. The strongest argument against supersymmetry is that neither the Higgs particle nor its supersymmetric partners have yet been found. Although the discovery of supersymmetric partners might be imminent, it is not entirely clear why, if supersymmetry solves the hierarchy problem, they haven’t already been observed. Experimenters have reached energies of a few hundred GeV. Although superpartners could certainly be a bit heavier, there really is no reason for them to be. In fact, lighter superpartners are better from the perspective of solving the hierarchy problem. Why, if supersymmetry solves the hierarchy problem, haven’t superpartners already been found?

On the theoretical side, supersymmetry is not completely compelling because big questions remain about how it is broken. We know that it must be broken spontaneously, but, as in the case of the Standard Model and weak force symmetry, we don’t yet know which particles are responsible. Many fascinating ideas have been suggested, but a completely satisfactory four-dimensional theory has yet to be proposed.

When I first learned about supersymmetry, it almost seemed too easy from a model building perspective. It looked as though supersymmetric theories could contain random unrelated masses, since quantum contributions were absent. Even if we didn’t know why very disparate masses should appear, they wouldn’t cause any trouble. This was very disappointing from a model building perspective because
nothing seemed to give any clue about the as yet undetermined underlying theory. And it also was pretty boring, since building models didn’t seem to present any challenges.

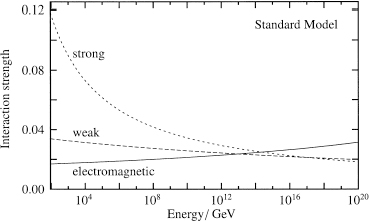
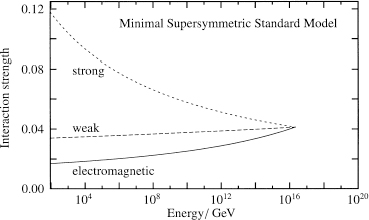
Figure 66.
The upper plot represents the strengths of the electromagnetic, weak, and strong forces as a function of energy in the Standard Model. The curves approach one another, but do not meet in a single point. The lower plot represents the strengths of the same three forces as a function of energy in the supersymmetric extension of the Standard Model. The strength of the three forces is the same at high energy, indicating that the three forces might actually unify into a single force.

But then I learned about the supersymmetry
flavor problem
, which tells us that this isn’t true; in fact, it’s very difficult to make the concrete details of a theory with broken supersymmetry work. The problem is a bit subtle, but it’s important nonetheless. The flavor problem is the major obstacle to a simple theory of supersymmetry
breaking. All new theories of supersymmetry breaking focus on this problem, and Chapter 17 will show why supersymmetry breaking in extra dimensions is a potential solution.

Recall that the flavors of Standard Model fermions are the three different fermions of the three different generations that have identical charges but different masses: the up, charm, and top quarks, or the electron, muon, and tau, for example. In the Standard Model, the identities of these particles do not change. For example, muons never directly interact with electrons: they interact only indirectly through the exchange of a weak gauge boson. Although muons can decay into electrons, that is only because the decay produces a muon neutrino and an electron antineutrino as well (see Figure 53, Chapter 7). The muon never converts to an electron directly without the emission of the associated neutrinos.

A physicist’s way of expressing this definite identity of a particular lepton type is to say that electron or muon number is conserved. We assign positive electron number to an electron and an electron neutrino, and a negative electron number to a positron and an electron antineutrino. And we assign a positive muon number to a muon and a muon neutrino, and a negative muon number to an antimuon and a muon antineutrino. If muon and electron numbers are preserved, a muon could never decay into an electron and a photon, since we would start with a positive muon number and a zero electron number and end up with a positive electron number and a zero muon number. And in fact, no one has ever seen such a decay. So far as we can tell, electron and muon number are preserved by all particle interactions.

In a supersymmetric theory, electron and muon number conservation would tell us that although an electron and a selectron can interact via the weak force, as can a muon and a smuon, an electron would never interact directly with a smuon. If, for any reason, an electron were paired with a smuon or a muon with a selectron, interactions would be generated that are not seen in nature, such as the muon decaying into an electron and a photon.

The problem is that although such flavor-changing
interactions
don’t occur in a truly supersymmetric theory, once supersymmetry is broken, nothing guarantees that muon and electron number remain conserved. Supersymmetry interactions in a theory with broken
supersymmetry can change the number of electrons and muons—contradicting what we know from experiments. This is because massive bosonic superpartners do not have the strong sense of identity of their partner fermions. The masses they have in a supersymmetric theory allow the bosonic superpartners to get all mixed up. Not only a smuon, but also a selectron would be paired with a muon, for example. But the pairing of a selectron and a muon would yield all sorts of decays that we know don’t occur. In any correct theory of nature, interactions that change muon or electron number would have to be very weak (or nonexistent) since such interactions have never been observed.

The quarks would suffer similar problems. Quark flavor would not be conserved when supersymmetry is broken, and would lead to the dangerous intermingling of generations that Ike feared in the opening story. Some mixing of quarks does happen in nature, but to a far lesser degree than supersymmetry-breaking theories would predict.

Theories of supersymmetry breaking face the formidable challenge of explaining why such flavor-changing interactions do not occur far too often. Unfortunately for supersymmetric theories, most of them cannot explain the absence of flavor-changing effects like these. This is impermissible: such mixing must be forbidden if the theories are to correspond to nature.

If this problem seems obscure to you, you might take some comfort from the fact that many physicists originally felt the same way and also didn’t consider the supersymmetry flavor problem to be all that important. To simplify enormously, the split in thinking fell along geographic lines: Europeans didn’t care as much as Americans. Those of us who had already spent years thinking about the flavor problem in other contexts knew how difficult it could be to solve. But many others originally ignored the anarchic principle’s implications and didn’t see why we should worry. In fact, after returning from the International Supersymmetry Conference in Ann Arbor, Michigan, in 1994, David B. Kaplan, a wonderful physicist (and my first collaborator in graduate school) now at the Institute for Nuclear Theory in Seattle, described to me how frustrated he was after he explained his proposed solution to the flavor problem to the audience there, but only
afterwards discovered how few people thought there was a problem in the first place!

This all changed rather quickly. Most people now acknowledge the severity of the flavor problem. It is very difficult to find theories of supersymmetry breaking that give all the necessary superpartner masses without compromising particle identities. How to break supersymmetry but prevent flavor changing is a crucial challenge if supersymmetry is to succeed in addressing the hierarchy problem. The loss of muon and electron (and quark) number conservation might sound technical, but it really is the bugaboo of supersymmetry breaking. It is just very difficult to prevent superpartners from turning into each other. Symmetries are in general powerless to prevent it.

So once again we return to our theme: theories with symmetry are elegant, but the broken symmetry that describes the world we see should be equally elegant. How and why is supersymmetry broken? We will have completed the theoretical challenge of understanding supersymmetric theories only when we have a compelling model of supersymmetry breaking.

This is not to say that supersymmetry is necessarily wrong, or even that it has nothing to do with the hierarchy problem. It does, however, mean that an additional ingredient is required for supersymmetric theories of the world to be successful. We’ll soon see that the extra ingredient might be extra dimensions.

What to Remember

• Supersymmetry
  essentially doubles the particle spectrum. For every boson in the theory, supersymmetry introduces a partnered fermion, and for every fermion, it introduces a partnered boson.
  
• Quantum mechanical effects make it difficult (without supersymmetry) to keep the Higgs particle light enough for the Standard Model to work. Until the advent of extra-dimensional theories, supersymmetry was the only known way to address this problem.
  
• Supersymmetry won’t necessarily tell us why the Higgs particle is light, but it does address the hierarchy problem by making a light Higgs particle a plausible assumption.
  
• The large virtual contributions that Standard Model particles and their superpartners make to the Higgs particle’s mass add up to zero. Therefore a light Higgs particle is not problematic in a supersymmetric theory.
  
• Even though supersymmetry might solve the hierarchy problem, it cannot be exact. If it were, superpartners would have the same masses as Standard Model particles, and we would have already found experimental evidence of supersymmetry.
  
• Superpartners
  , should they exist, must be more massive than their Standard Model partners. Because high-energy colliders can produce particles only up to a certain mass, these colliders might not yet have had enough energy to produce them. This would explain why we have not yet seen them.
  
• Once supersymmetry is broken,
  flavor-changing interactions
  can occur. These are processes that change quarks or leptons into quarks or leptons of another generation (that is, ones that are heavier or lighter) with the same charges. These are very strange processes—they change the identity of known particles, and they occur only rarely in nature. But most theories of broken supersymmetry predict that they should occur very often—more often than we see in experiments.