Warped Passages (16 page)

Einstein’s theory of special relativity, with its radical revision of the concepts of space and time, was a major leap. Peter Galison,
†
a physicist and historian of science, suggests that it was not only the aether theory that put Einstein on the right track, but Einstein’s job at the time. Galison reasoned that Einstein, who grew up in Germany and worked at the patent office in Bern, Switzerland, must have had time and time coordination on his mind. Anyone who has traveled in Europe knows that precision is valued highly in countries such as Switzerland and Germany, which has the happy consequence that passengers can count on the trains to run on time. Einstein worked in the patent office between 1902 and 1905, during an era when train travel was becoming increasingly important, and coordinating time was at the forefront of new technology. In the early 1900s, Einstein was very likely thinking about real-world problems, such as how to coordinate the time at one train station with that at another.
Of course, Einstein did not need to develop relativity to solve the problem of coordinating real trains. (For those of us accustomed to the frequently delayed American trains, coordinated time might sound exotic in any case.
‡
) But coordinating time raised some interesting questions. Time coordination of relativistically moving trains is not a straightforward problem. If I were to coordinate my watch with someone on a moving train, I would need to account for the time delay of a signal traveling between us because light has a finite speed. Coordinating my watch with that of the person sitting next to me
would not be the same as coordinating watches with someone far away.
*
Einstein’s critical insight, the one that led him to special relativity, was that ideas about time had to be reformulated. According to Einstein, space and time could no longer be considered independently. Although they are not the same thing—time and space are clearly different—the quantities you measure depend on the speed at which you are traveling. Special relativity was the result of this insight.
Bizarre as they are, one can derive all of Einstein’s novel consequences of special relativity from two postulates. To state them, we need to understand the meaning of
inertial frames
—a particular category of reference frames. Let’s first choose any frame of reference that moves at constant velocity (speed and direction); the one that’s at rest is often a good one. The inertial frames would then be those that are moving at fixed velocity with respect to that first one—someone running or driving by at constant speed, for example.
Einstein’s postulates then state that:
The laws of physics are the same in all inertial frames.
The speed of light,
c
, is the same in any inertial frame.
The two postulates tell us that Newton’s laws are incomplete. Once we accept Einstein’s postulates, we have no choice but to replace Newton’s laws with new physical laws that are consistent with these rules.
8
The laws of special relativity that follow lead to all the surprising consequences you might have heard of, such as time dilation, the observer dependence of simultaneity, and Lorentz contraction of a moving object. The new laws should look very much like the old classical physics laws when applied to objects moving at speeds that are small compared with the speed of light. But when applied to something moving very fast, at or near the speed of light, the difference
between the Newtonian and special relativity formulations should become apparent.
For example, in Newtonian mechanics speeds are simply added together. A car driving towards yours on the freeway approaches you at a speed that’s the sum of its speed and yours. Similarly, if someone throws a ball at you from the platform while you are on a moving train, the ball’s speed appears to be the sum of the speed of the ball itself plus the speed of the moving train. (A former student of mine, Witek Skiba, can attest to this fact. Witek was nearly knocked out when he was hit by a ball that someone threw at the approaching train he was riding.)
According to Newtonian physics, the speed of a beam of light directed at a moving train should be the sum of the speed of light and the speed of the moving train. But this can’t be true if the speed of light is constant, as Einstein’s second postulate asserts. If the speed of light is always the same, then the speed of the beam aimed at the moving train will be identical to the speed of a light beam that approaches you when you’re standing still on the ground. Even though it runs counter to the intuition gained from your experience of the slow speeds you encounter in daily life, light speed is constant, and in special relativity speeds don’t simply add up as they do in Newtonian physics. Instead, you add speeds according to a relativistic formula that follows from Einstein’s postulates.
Many of special relativity’s implications don’t jibe with our familiar notions of time and space. Special relativity treats time and space differently than they had been treated before in Newtonian mechanics, and this is what gives rise to many of its counterintuitive results. Time and space measurements depend on speed and get mixed up in systems that move relative to each other. Nonetheless, surprising as they are, once you accept the two postulates then a different notion of space and time is an inevitable consequence.
Here’s one argument why. Imagine two identical ships with identical masts. One ship is docked by the shore, while the other is moving away. Also imagine that the captains of the two ships synchronized their watches when the first ship sailed off.
Now suppose that the two captains do a rather odd thing: each decides to measure time on her ship by placing a mirror at the top of
the mast and a second mirror at the bottom, shining a light from the bottom mirror to the top one, and measuring the number of times light hits the mirror and returns. As a practical matter, of course, this would be absurd, since light would cycle up and down far too frequently to count. But bear with me, and imagine that the captains can count extraordinarily fast; I’ll be using this somewhat contrived example to argue that time stretches out on the moving ship.
If each captain knows how long it takes for light to cycle once, she can calculate the passage of time by multiplying the light-cycle time by the number of times light cycles up and down between the mirrors. Now suppose, though, that instead of using her own stationary mirror clock, the captain on the docked ship measures time by the number of times the light on the moving ship hits the mast’s mirror and returns.
Now from the perspective of the captain on the moving ship, the light simply goes straight up and down. However, from the perspective of the captain on the docked ship, the light has to travel farther (in order to cover the distance traveled by the moving ship—see Figure 35). But—and this is the counterintuitive part—the speed of light is constant. It is the same for the light sent to the top of the mast on the docked ship as it is for the light sent to the top of the mast on the moving ship. Since speed measures distance traveled over time, and the speed of light for the moving ship is the same as the speed of light for the stationary one, the moving mirror clock has to “tick” at a slower rate to compensate for the longer distance the moving light
has to travel. This very counterintuitive conclusion—that moving and stationary clocks must tick at different rates—follows from the fact that the speed of light in a moving reference frame is the same as the speed of light in a stationary one. And although this is a funny way to measure time, the same conclusion—that moving clocks run slower—would hold true independently of how time is measured. If the captains had watches on, they would observe the same thing (again, with the caveat that for normal speeds, the effect would be tiny).
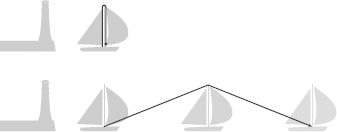
Figure 35.
The path of a light beam that bounces off the top of a mast of a stationary ship and of a moving one. The stationary observer (in a boat by the shore or in a lighthouse) would see a longer path in the second case.
While the above example is artificial, the phenomenon described produces genuinely measurable effects. For example, special relativity gives rise to the different time experienced by fast-moving objects—the phenomenon known as time dilation.
Physicists measure time dilation when they study elementary particles produced at colliders or in the atmosphere, which travel at relativistic speeds—speeds approaching that of light. For example, the elementary particle called a muon has the same charge as an electron, but is heavier and can decay (that is, it can turn into other, lighter particles). The muon’s lifetime, the time before it decays, is only 2 microseconds. If a moving muon had the same lifetime as a stationary one, it would be able to travel only about 600 meters before it disappeared. But muons manage to make it all the way through our atmosphere, and in colliders, to the edges of large detectors, because their near-light-speed velocity makes them appear to us much longer-lived. In the atmosphere, muons travel at least ten times further than they would in a universe based on Newtonian principles. The very fact that we see these muons at all shows us that time dilation (and special relativity) gives rise to true physical effects.
Special relativity is important both because it was a dramatic deviation from classical physics and because it was essential to the development of general relativity and quantum field theory, both of which play a significant role in more recent developments. Because I won’t use specific special relativity predictions when I discuss particle physics and extra-dimensional models later on, I’ll resist the urge to go into all the fascinating consequences of special relativity, such as why simultaneity depends on whether an observer is moving and how the sizes of moving objects are different from when they are at rest.
Instead, we’ll delve into another dramatic development, namely general relativity, which will be critical when we consider string theory and extra dimensions later on.
The Principle of Equivalence: General Relativity Begins
Einstein wrote down his theory of special relativity in 1905. In 1907, while working on a paper that summarized his recent work on the subject, he found himself already questioning whether the theory could apply to all situations. He noticed two major omissions. For one thing, physical laws looked the same only in certain special inertial reference frames—those that moved at fixed velocity with respect to each other.
In special relativity, these inertial reference frames occupied a privileged position. The theory left out any reference frame that was accelerating. If you pressed the accelerator while driving your car, you would no longer be in one of the special reference frames where the laws of special relativity apply. That’s what’s “special” in special relativity: the “special” inertial frames are only a small subset of all possible reference frames. For someone convinced that no one’s reference frame is special, it was a big problem that the theory singled out inertial reference frames.
Einstein’s second misgiving concerned gravity. Although he had figured out how objects respond to gravity in some situations, he still hadn’t come up with formulas for determining the gravitational field in the first place. The form of the gravitational force law was known in some simpler settings, but Einstein wasn’t yet able to deduce the field for every possible distribution of matter.
Between 1905 and 1915, in a sometimes grueling exploration, Einstein addressed these problems. The result was general relativity. He centered his new theory around the
equivalence principle
, which states that the effects of acceleration cannot be distinguished from those of gravity. All the laws of physics would look the same to an accelerating observer as they would to a stationary observer placed in a gravitational field that accelerates everything in the stationary frame
with an acceleration of the same magnitude—but in the opposite direction—as the original observer’s acceleration. In other words, you wouldn’t have any way of distinguishing uniform acceleration from standing still in a gravitational field. According to the principle of equivalence, there is no measurement that would distinguish between these two situations. An observer could never know which situation he was in.
The equivalence principle follows from the equivalence of
inertial
and
gravitational mass
, two quantities that in principle could have been different from each other. Inertial mass determines how an object will respond to any force—how much the object would accelerate if you applied that force. The role of inertial mass is summarized in Newton’s second law of motion,
F
=
ma
, which says that if you apply a force of magnitude
F
to an object with mass
m
, you will produce an acceleration
a
. Newton’s famous second law tells us that a given force produces smaller acceleration on an object that has bigger inertial mass, which is probably very familiar to you from experience. (If you shove a footstool, it will go further and faster than if you shove a grand piano just as hard.) Notice that this law applies for any sort of force—the force of electromagnetism, for example. It can apply in situations that have nothing whatsoever to do with gravity.