The Sleepwalkers (246 page)

It
is
only
by
bringing
into
the
open
the
inherent
contradictions,
and
the
metaphysical
implications
of
Newtonian
gravity,
that
one
is
able
to
realize
the
enormous
courage
–
or
sleepwalker's
assurance
–
that
was
needed
to
use
it
as
the
basic
concept
of
cosmology.
In
one
of
the
most
reckless
and
sweeping
generalizations
in
the
history
of
thought,
Newton
filled
the
entire
space
of
the
universe
with
interlocking
forces
of
attraction,
issuing
from
all
particles
of
matter
and
acting
on
all
particles
of
matter,
across
the
boundless
abysses
of
darkness.

But
in
itself
this
replacement
of
the
anima
mundi
by
a
gravitatio
mundi
would
have
remained
a
crank
idea
or
a
poet's
cosmic
dream;
the
crucial
achievement
was
to
express
it
in
precise
mathematical
terms,
and
to
demonstrate
that
the
theory
fitted
the
observed
behaviour
of
the
cosmic
machinery
–
the
moon's
motion
round
the
earth
and
the
planets'
motions
round
the
sun.

5.
The Final Synthesis

His
first
step
was
to
do
in
imagination
what
history
had
failed
to
achieve:
to
bring
Kepler
and
Galileo
together.
More
precisely:
to
join
one
half
of
Kepler
to
one
half
of
Galileo,
and
to
discard
each
redundant
half.

The
meeting
place
was
the
moon.
Young
Jeremiah
Horrocks
–
the
English
prodigy
who
died
at
twenty-one
–
had
applied
Kepler's
Laws
to
the
orbit
of
the
moon.
This
provided
Newton
with
one
half
of
the
synthesis.
The
second
half
he
found
in
Galileo's
Laws
of
the
motion
of
projectiles
in
the
immediate
vicinity
of
the
earth.
Newton
identified
the
Keplerian
orbit
of
the
moon
with
the
Galilean
orbit
of
a
projectile
,
which
was
constantly
falling
downward
towards
the
earth,
but
was
unable
to
reach
it,
owing
to
its
fast
forward
motion.
In
his
System
of
the
World
,
his
process
of
reasoning
is
described
as
follows:

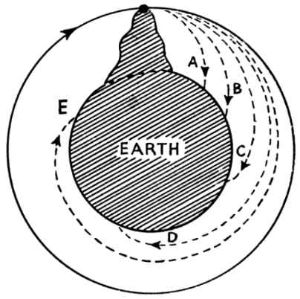
If
a
projectile
is
fired
from
the
top
of
a
mountain,
it
will
be
deflected
from
its
straight
path
by
the
earth's
attraction.
According
to
the
initial
velocity
imparted
to
it,
it
will
follow
the
curves
A,
B,
C,
D
or
E;
and
if
the
initial
velocity
exceeds
a
certain
critical
value,
the
projectile
will
describe
a
circle
or
an
ellipse
"and
return
to
the
mountain
from
which
it
was
projected".
Moreover,
according
to
Kepler's
Second
Law,
"its
velocity
when
it
returns
to
the
mountain
will
be
no
less
than
it
was
at
first:
and
retaining
the
same
velocity,
it
will
describe
the
same
curve
over
and
over
by
the
same
law
...
and
go
on
revolving
through
the
heavens
just
as
the
planets
do
in
their
orbs."
In
other
words,
Newton,
by
thought-experiment,
created
an
artificial
satellite
nearly
three
hundred
years
before
technology
was
able
to
implement
it.

Thus
the
basic
idea
of
Newton's
celestial
mechanics
is
the
interaction
of
two
forces:
the
force
of
gravity,
which
pulls
the
planet
towards
the
sun,
and
the
centrifugal
force,
which
counteracts
it.
The
usual
way
to
demonstrate
the
idea
is
to
whirl
around
a
stone
at
the
end
of
a
string.
The
force
which
keeps
the
string
taut
is
the
stone's
centrifugal
force;
the
cohesion
of
the
string
which
holds
the
stone
captive
in
its
orbit
represents
the
gravitational
attraction.

But
why
does
the
planet
follow
an
elliptical,
instead
of
a
circular
path?
To
put
it
in
a
simple
way,
because
when
I
whirl
a
stone
round,
the
length
of
the
string
is
fixed,
and
it
won't
stretch
–
whereas
the
sun's
attractive
pull
varies
according
to
distance.
Accordingly,
the
stone
goes
round
in
a
perfect
circle,
whereas
the
planet
would
go
round
in
a
perfect
circle
only
if
its
tangential
velocity,
and
the
resulting
centrifugal
force,
happened
just
exactly
to
counterbalance
the
sun's
attraction.
If
its
speed
is
smaller
than
the
required
amount,
the
planet
will
revolve
round
the
sun
in
narrowing
spiral
turns
and
eventually
fall
into
it,
as
a
meteorite
spirals
down
to
the
earth.
If
the
planet's
velocity
happens
to
be
"just
right",
it
will
conform
to
Aristotle
and
revolve
in
a
perfect
circle.
If,
however,
its
speed
is
greater
than
required,
the
planet
will
move
not
in
a
circle
but
in
an
ellipse.
The
greater
the
tangential
velocity
in
relation
to
the
attracting
force,
the
more
elongated
the
ellipse
will
be;
until
one
end
of
it
will
be
stretched
open
toward
infinity,
as
it
were,
and
the
ellipse
will
change
into
a
parabola
–
the
assumed
path
of
certain
comets
which
come
from
the
depth
of
space,
are
deflected
from
their
course
by
the
sun,
but
not
sufficiently
to
be
captured,
and
recede
again
into
infinity.