The Sleepwalkers (187 page)

The
Harmony
of
the
World
is
the
continuation
of
the
Cosmic
Mystery
,
and
the
climax
of
his
lifelong
obsession.
What
Kepler
attempted
here
is,
simply,
to
bare
the
ultimate
secret
of
the
universe
in
an
all-embracing
synthesis
of
geometry,
music,
astrology,
astronomy
and
epistemology.
It
was
the
first
attempt
of
this
kind
since
Plato,
and
it
is
the
last
to
our
day.
After
Kepler,
fragmentation
of
experience
sets
in
again,
science
is
divorced
from
religion,
religion
from
art,
substance
from
form,
matter
from
mind.

The
work
is
divided
into
five
books.
The
first
two
deal
with
the
concept
of
harmony
in
mathematics;
the
following
three
with
the
applications
of
this
concept
to
music,
astrology
and
astronomy,
in
that
order.

What
exactly
does
he
mean
by
"harmony"?
Certain
geometrical
proportions
which
he
finds
reflected
everywhere,
the
archetypes
of
universal
order,
from
which
the
planetary
laws,
the
harmonies
of
music,
the
drift
of
the
weather,
and
the
fortunes
of
man
are
derived.
These
geometrical
ratios
are
the
pure
harmonies
which
guided
God
in
the
work
of
Creation;
the
sensory
harmony
which
we
perceive
by
listening
to
musical
consonances
is
merely
an
echo
of
it.
But
that
inborn
instinct
in
man
which
makes
his
soul
resonate
to
music,
provides
him
with
a
clue
to
the
nature
of
the
mathematical
harmonies
which
are
at
its
source.
The
Pythagoreans
had
discovered
that
the
octave
originates
in
the
ratio
1:2
between
the
length
of
the
two
vibrating
strings,
the
fifth
in
the
ratio
of
2:3,
the
fourth
in
3:4,
and
so
on.
But
they
went
wrong,
says
Kepler,
when
they
sought
for
an
explanation
of
this
marvellous
fact
in
occult
number-lore.
The
explanation
why
the
ratio
3:5,
for
instance,
gives
a
concord,
but
3:7
a
discord,
must
be
sought
not
in
arithmetical,
but
in
geometrical
considerations.
Let
us
imagine
the
string,
whose
vibrations
produce
the
sound,
bent
into
a
circle
with
its
ends
joined
together.
Now
a
circle
can
be
most
gratifyingly
divided
by
inscribing
into
it
symmetrical
figures
with
varying
numbers
of
sides.
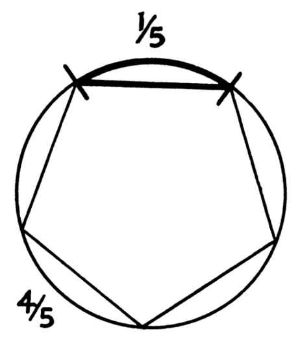
Thus
the
side
of
an
inscribed
Pentagon
will
divide
the
circumference
into
parts
which
are
to
the
whole
circle
as
1/5
and
4/5
respectively
–
both
consonant
chords.

But
a
septagon
will
produce
ratios
of
1/7
and
6/7
–
both
discords.
Why?
The
answer,
according
to
Kepler,
is:
because
the
pentagon
can
be
constructed
by
compass
and
ruler,
but
the
septagon
not
.
Compass
and
ruler
are
the
only
permissible
tools
in
classical
geometry.
But
geometry
is
the
only
language
which
enables
man
to
understand
the
working
of
the
divine
mind.
Therefore
figures
which
cannot
be
constructed
by
compass
and
ruler
–
such
as
the
septagon,
the
11,
13
or
17-sided
polygons
–
are
somehow
unclean,
because
they
defy
the
intellect.
They
are
inscibilis
,
unknowable,
¹²
inefabilis
,
unspeakable,
non-entia
,
non-existences.
"Therein
lies
the
reason,"
Kepler
explains,
"why
God
did
not
employ
the
septagon
and
the
other
figures
of
this
species
to
embellish
the
world."

Thus
the
pure
archetypal
harmonies,
and
their
echoes,
the
musical
consonances,
are
generated
by
dividing
the
circle
by
means
of
construable,
regular
polygons;
whereas
the
"unspeakable"
polygons
produce
discordant
sounds,
and
are
useless
in
the
scheme
of
the
universe.
To
the
obsession
with
the
five
perfect
solids
was
now
added
the
twin
obsession
with
the
perfect
polygons.
The
former
are
three-dimensional
bodies
inscribed
into
the
sphere,
the
latter
are
two-dimensional
shapes
inscribed
into
the
circle.
There
is
an
intimate,
mystical
connection
between
the
two:
the
sphere,
it
will
be
remembered,
is
for
Kepler
the
symbol
of
the
Holy
Trinity;
the
two-dimensional
plane
symbolizes
the
material
world;
the
intersection
of
sphere
and
plane,
the
circle,
pertains
to
both,
and
symbolizes
the
dual
nature
of
man
as
body
and
spirit.