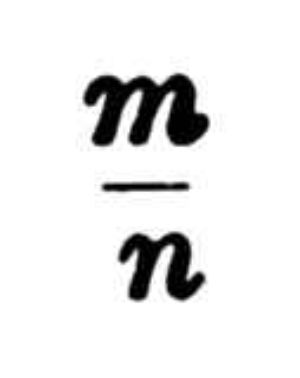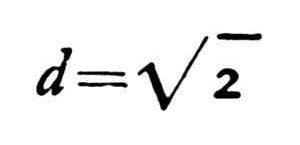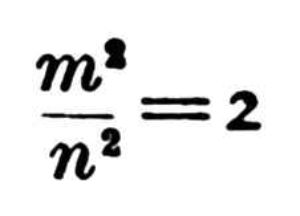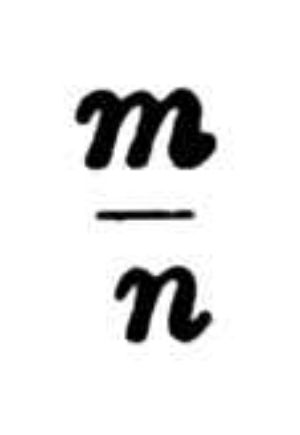The Sleepwalkers (15 page)

–
the
square
root
of
2
–
which
could
not
be
fitted
into
any
dot-diagram.
And
such
numbers
were
common:
they
are,
for
instance,
represented
by
the
diagonal
of
any
square.
Let
the
side
of
the
square
be
called
a
,
and
the
diagonal
d
.
It
can
be
proved
that
if
I
assign
to
a
any
precise
numerical
value,
then
it
becomes
impossible
to
assign
a
precise
numerical
value
to
d
.
The
side
and
the
square
are
"incommensurable";
their
ratio
a/d
cannot
be
represented
by
any
real
numbers
or
fractions
thereof;
it
is
an
"irrational"
number;
it
is
both
odd
and
even
at
the
same
time.
^*
I
can
easily
draw
the
diagonal
of
a
square,
but
I
cannot
express
its
length
in
numbers
–
I
cannot
count
the
number
of
dots
it
contains.
The
point-to-point
correspondence
between
arithmetic
and
geometry
has
broken
down
–
and
with
it
the
universe
of
numbershapes.

____________________

It
is
said
that
the
Pythagoreans
kept
the
discovery
of
irrational
numbers
–
they
called
them
arrhētos
,
unspeakable
–
a
secret,
and
that
Hippasos,
the
disciple
who
let
the
scandal
leak
out,
was
put
to
death.
There
is
also
another
version,
in
Proclos:
¹¹

"It
is
told
that
those
who
first
brought
out
the
irrationals
from
concealment
into
the
open
perished
in
shipwreck,
to
a
man.
For
the
unutterable
and
the
formless
must
needs
be
concealed.
And
those
who
uncovered
and
touched
this
image
of
life
were
instantly
destroyed
and
shall
remain
forever
exposed
to
the
play
of
the
eternal
waves."

Yet,
Pythagoreanism
survived.
It
had
the
elastic
adaptability
of
all
truly
great
ideological
systems
which,
when
some
part
is
knocked
out
of
them,
display
the
self-regenerating
powers
of
a
growing
crystal
or
a
living
organism.
The
mathematization
of
the
world
by
means
of
atom-like
dots
proved
a
premature
shortcut;
but
on
a
higher
turn
of
the
spiral,
mathematical
equations
proved
once
again
the
most
serviceable
symbols
for
representing
the
physical
aspect
of
reality.
We
shall
meet
with
further
examples
of
prophetic
intuition
supported
by
the
wrong
reasons;
and
we
shall
find
that
they
are
rather
the
rule
than
the
exception.