The Information (54 page)

3751…
This looks random. Statistically each digit appears with the expected frequency (one in ten); likewise each pair of digits (one in a hundred), each triplet, and so on. A statistician would say it appears to be “normal,” as far as anyone can tell. The next digit is always a surprise. The works of Shakespeare will be in there, eventually. But someone might recognize this as a familiar number, Π. So it is not random after all.
But why do we say Π is not random? Chaitin proposed a clear answer: a number is not random if it is computable—if a definable computer program will generate it. Thus computability is a measure of randomness.
For Turing computability was a yes-or-no quality—a given number either is or is not. But we would like to say that some numbers are more
random than others—they are less patterned, less orderly. Chaitin said the patterns and the order express computability. Algorithms generate patterns. So we can gauge computability by looking at
the size of the algorithm
. Given a number—represented as a string of any length—we ask, what is the length of the shortest program that will generate it? Using the language of a Turing machine, that question can have a definite answer, measured in bits.
Chaitin’s algorithmic definition of randomness also provides an algorithmic definition of information: the size of the algorithm measures how much information a given string contains.
Looking for patterns—seeking the order amid chaos—is what scientists do, too. The eighteen-year-old Chaitin felt this was no accident. He ended this first paper by applying algorithmic information theory to the process of science itself. “Consider a scientist,” he proposed, “who has been observing a closed system that once every second either emits a ray of light or does not.”
He summarizes his observations in a sequence of 0s and 1s in which a 0 represents “ray not emitted” and a 1 represents “ray emitted.” The sequence may start
0110101110 …
and continue for a few thousand more bits. The scientist then examines the sequence in the hope of observing some kind of pattern or law. What does he mean by this? It seems plausible that a sequence of 0s and 1s is patternless if there is no better way to calculate it than just by writing it all out at once from a table giving the whole sequence.
♦
But if the scientist could discover a way to produce the same sequence with an algorithm, a computer program significantly shorter than the sequence, then he would surely know the events were not random. He would say that he had hit upon a theory. This is what science always seeks: a simple theory that accounts for a large set of facts and allows for
prediction of events still to come. It is the famous Occam’s razor. “We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances,” said Newton, “for nature is pleased with simplicity.”
♦
Newton quantified
mass
and
force
, but
simplicity
had to wait.
Chaitin sent his paper to the
Journal of the Association for Computing Machinery
. They were happy to publish it, but one referee mentioned that he had heard rumors of similar work coming from the Soviet Union. Sure enough, the first issue of a new journal arrived (after a journey of months) in early 1966: ,
,
Problems of Information Transmission
. It contained a paper titled “Three Approaches to the Definition of the Concept ‘Amount of Information,’ ” by A. N. Kolmogorov. Chaitin, who did not read Russian, had just time to add a footnote.
Andrei Nikolaevich Kolmogorov was the outstanding mathematician of the Soviet era. He was born in Tambov, three hundred miles southeast of Moscow, in 1903; his unwed mother, one of three sisters Kolmogorova, died in childbirth, and his aunt Vera raised him in a village near the river Volga. In the waning years of tsarist Russia, this independent-minded woman ran a village school and operated a clandestine printing press in her home, sometimes hiding forbidden documents under baby Andrei’s cradle.
♦
Moscow University accepted Andrei Nikolaevich as a student of mathematics soon after the revolution of 1917. Within ten years he was proving a collection of influential results that took form in what became the theory of probability. His
Foundations of the Theory of Probability
, published in Russian in 1933 and in English in 1950, remains the modern classic. But his interests ranged widely, to physics and linguistics as well as other fast-growing branches of mathematics. Once he made a foray into genetics but drew back after a dangerous run-in with Stalin’s favorite pseudoscientist, Trofim Lysenko. During World War II
Kolmogorov applied his efforts to statistical theory in artillery fire and devised a scheme of stochastic distribution of barrage balloons to protect Moscow from Nazi bombers. Apart from his war work, he studied turbulence and random processes. He was a Hero of Socialist Labor and seven times received the Order of Lenin.
He first saw Claude Shannon’s
Mathematical Theory of Communication
rendered into Russian in 1953, purged of its most interesting features by a translator working in Stalin’s heavy shadow. The title became
Statistical Theory of Electrical Signal Transmission
. The word
information
,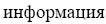 , was everywhere replaced with
, was everywhere replaced with ,
,
data
. The word
entropy
was placed in quotation marks to warn the reader against inferring a connection with entropy in physics. The section applying information theory to the statistics of natural language was omitted entirely. The result was technical, neutral, juiceless, and thus unlikely to attract interpretation in the terms of Marxist ideology.
♦
These were serious concerns; “cybernetics” was initially defined in the
Short Philosophical Dictionary
(standard reference of ideological orthodoxy) as a “reactionary pseudoscience” and “an ideological weapon of imperialist reaction.” Kolmogorov leapt upon Shannon’s paper nonetheless; he, at least, was unafraid to use the word
information
. Working with his students in Moscow, he put forth a rigorous mathematical formulation of information theory, with definitions of the fundamental concepts, careful proofs, and new discoveries—some of which, he soon learned to his sorrow, had appeared in Shannon’s original paper but had been omitted from the Russian version.
♦
In the Soviet Union, still moderately isolated from the rest of the world’s science, Kolmogorov was well placed to carry the banner of information. He was in charge of all mathematics in the
Great Soviet Encyclopedia
, choosing the authors, editing the articles, and writing much of it himself. In 1956 he delivered a long plenary report on the theory of information transmission to the Soviet Academy of Sciences. His colleagues thought this was a bit “addled”—that Shannon’s work was “more technology than mathematics,”
♦
as Kolmogorov recalled it afterward. “It
is true,” he said, “that Shannon left to his successors the rigorous ‘justification’ of his ideas in some difficult cases. However, his mathematical intuition was amazingly precise.” Kolmogorov was not as enthusiastic about cybernetics. Norbert Wiener felt a kinship with him—they had both done early work on stochastic processes and Brownian motion. On a visit to Moscow, Wiener said, “When I read the works of Academician Kolmogorov, I feel that these are my thoughts as well, this is what I wanted to say. And I know that Academician Kolmogorov has the same feeling when reading my works.”
♦
But the feeling was evidently not shared. Kolmogorov steered his colleagues toward Shannon instead. “It is easy to understand that as a mathematical discipline cybernetics in Wiener’s understanding lacks unity,” he said, “and it is difficult to imagine productive work in training a specialist, say a postgraduate student, in cybernetics in this sense.”
♦
He already had real results to back up his instincts: a useful generalized formulation of Shannon entropy, and an extension of his information measure to processes in both discrete and continuous time.
Prestige in Russia was finally beginning to flow toward any work that promised to aid electronic communication and computing. Such work began almost in a void. Pragmatic electrical engineering barely existed; Soviet telephony was notoriously dismal, a subject for eternally bitter Russian humor. As of 1965, there was still no such thing as direct long-distance dialing. The number of toll calls nationally had yet to surpass the number of telegrams, a milestone that had been reached in the United States before the end of the previous century. Moscow had fewer telephones per capita than any major world city. Nonetheless, Kolmogorov and his students generated enough activity to justify a new quarterly journal,
Problems of Information Transmission
, devoted to information theory, coding theory, theory of networks, and even information in living organisms. The inaugural issue opened with Kolmogorov’s “Three Approaches to the Definition of the Concept ‘Amount of Information’”—almost a manifesto—which then began its slow journey toward the awareness of mathematicians in the West.
“At each given moment there is only a fine layer between the ‘trivial’ and the impossible,”
♦
Kolmogorov mused in his diary. “Mathematical discoveries are made in this layer.” In the new, quantitative view of information he saw a way to attack a problem that had eluded probability theory, the problem of randomness. How much information is contained in a given “finite object”? An object could be a number (a series of digits) or a message or a set of data.
He described three approaches: the combinatorial, the probabilistic, and the algorithmic. The first and second were Shannon’s, with refinements. They focused on the probability of one object among an ensemble of objects—one particular message, say, chosen from a set of possible messages. How would this work, Kolmogorov wondered, when the object was not just a symbol in an alphabet or a lantern in a church window but something big and complicated—a genetic organism, or a work of art? How would one measure the amount of information in Tolstoy’s
War and Peace
? “Is it possible to include this novel in a reasonable way in the set of ‘all possible novels’ and further to postulate the existence of a certain probability distribution in this set?”
♦
he asked. Or could one measure the amount of genetic information in, say, the cuckoo bird by considering a probability distribution in the set of all possible species?
His third approach to measuring information—the algorithmic—avoided the difficulties of starting with ensembles of possible objects. It focused on the object itself.
♦
♦
Kolmogorov introduced a new word for the thing he was trying to measure:
complexity
. As he defined this term, the complexity of a number, or message, or set of data is the inverse of simplicity and order and, once again, it corresponds to information. The simpler an object is, the less information it conveys. The more
complexity, the more information. And, just as Gregory Chaitin did, Kolmogorov put this idea on a solid mathematical footing by calculating complexity in terms of algorithms. The complexity of an object is the size of the smallest computer program needed to generate it. An object that can be produced by a short algorithm has little complexity. On the other hand, an object needing an algorithm every bit as long as the object itself has maximal complexity.