The Eternal Flame (53 page)

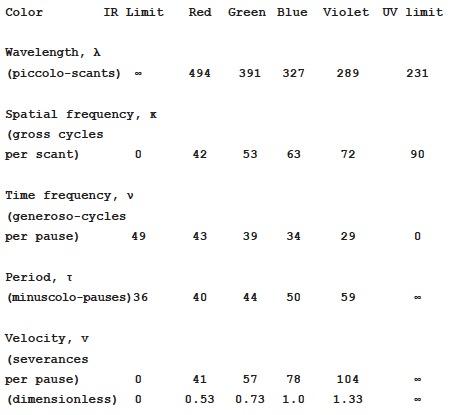
The smallest possible wavelength of light, λ
_min
, is about 231 piccolo-scants; this is for light with an infinite velocity, at the “ultraviolet limit”. The highest possible time frequency of light, ν
_max
, is about 49 generoso-cycles per pause; this is for stationary light, at the “infrared limit”.

Appendix 3:
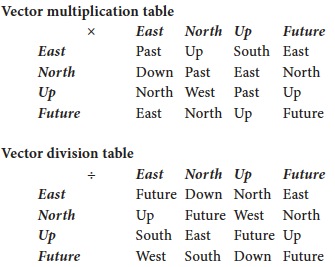
Vector multiplication
and division

The travelers on the
Peerless
have developed a way of multiplying and dividing four-dimensional vectors, turning these vectors into a fully fledged number system like the more familiar real and complex numbers. In our own culture, this system is known as the quaternions; it was discovered by William Hamilton in 1843. Just as the real numbers form a one-dimensional line and the complex numbers form a two-dimensional plane, the quaternions form a four-dimensional space, making them the ideal number system for four-dimensional geometry. In our universe the distinction between time and space prevents us making full use of the quaternions, but in the
Orthogonal
universe the geometry of four-space and the arithmetic of the quaternions fit together seamlessly.

In the version used on the
Peerless
, the principal directions in the four dimensions are called East, North, Up and Future, with opposites West, South, Down and Past. The Future direction takes the role of the number one: multiplying or dividing any vector by Future leaves the original vector unchanged. Squaring any of the other three principal directions—East, North and Up—always gives Past, or minus one, so this number system contains three independent square roots of minus one, compared to the single square root of minus one,
i
, in the complex numbers. (Of course squaring the opposite directions—West, South and Down—also gives Past, just as in the complex numbers squaring –
i
also gives minus one, but these aren’t counted as independent square roots.)

Multiplication in this system is non-commutative:
a
×
b
generally isn’t the same as
b
×
a
.

Every non-zero vector
v
has a unique reciprocal or inverse, written
v
^-1
, which is the vector for which:

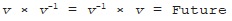
For example, East
^-1
= West, North
^-1
= South, Up
^-1
= Down and Future
^-1
= Future. In the first three cases the inverse of the vector is its opposite, but that’s not true in general.

When we divide vectors,
w
÷
v
is just multiplication (on the right side) by
v
^-1
:

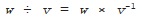
Because multiplication is non-commutative, we need to be careful with the order of vectors when we take inverses or perform division. Taking the inverse of two or more vectors multiplied together entails
reversing their order
:

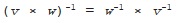
This reversal is necessary to ensure that the original vectors come together in the right sequence to give a final result of Future:

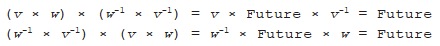
Similarly, when we divide by a product of vectors we need to reverse their order:

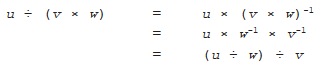
Although the tables only give the results for multiplying and dividing the four principal directions, the same operations can be applied to any vectors at all (with the exception that you can’t divide by the zero vector). A completely general vector can be formed by adding together various multiples of the principal directions:

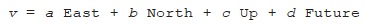
Here
a
,
b
,
c
and
d
are real numbers, and they can be positive, negative or zero. Let’s define another vector,
w
, using four other real numbers,
A
,
B
,
C
and
D
:

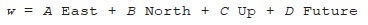
We can multiply
v
and
w
together by following the ordinary rules of algebra, taking care with the order in which we write the products of vectors: