The Case for Mars (39 page)

It can be seen that if chemical systems are used exclusively, then the mass ratio required to deliver dry mass to the asteroid belt from Earth is 14 times greater than from Mars. This implies a still (much) greater ratio of payload to takeoff mass ratio from Mars to Ceres than from Earth. In fact, looking at
Table 8.1
, we can safely say that useful trade between Earth and Ceres (or any other body in the main asteroid belt) using chemical propulsion is probably impossible, while from Mars it is relatively easy. We can also see that there is nearly a fivefold advantage in mass ratio delivering cargoes to the Earth’s Moon from Mars over doing it from Earth.

If nuclear electric propulsion is introduced, the story changes, but not much. Mars still has a sevenfold advantage in mass ratio over Earth as a port of departure for the main belt, which translates into a payload-to-takeoff-weight ratio nearly two orders of magnitude higher for Mars departure than for Earth.

TABLE 8.2
of Freighter Missions to the Main Asteroid Belt (tonnes)

But those are just mass ratios, and as noted above, this understates Mars’ advantage. Now let’s compare some end-to-end missions that go from either Earth or Mars to Ceres. This is shown in
Table 8.2
, with both all-chemical and combined chemical/NEP transportation systems considered. Both missions deliver 50 tonnes of cargo. In addition, both NEP and chemical systems have to carry fuel tanks whose mass I estimated at 7 percent of the propellant they carry. For surface-to-orbit vehicles, I employed methane/oxygen SSTO rockets, and assumed that the vehicles need to have a dry mass (for thermal protection, engines, landing gear, etc.) excluding tankage that is equal to their payload, or 50 tonnes. Chemical interplanetary transportation systems can be built flimsier, so I assigned them a dry inert mass excluding tankage equal to 20 percent of the payload. The NEP engines in
Table 8.2
require 10 megawatts of electricity (MWe) of power for delivery to Ceres from Mars and 30 MWe for delivery from Earth, with each NEP system massing 5 tonnes/MWe. The different power ratings give both systems about equal power/mass ratios. Nevertheless, the NEP system leaving Earth still has to burn its engine 2.4 times as long. If you wanted to increase the
power rating of the Earth-based NEP vessel so that its burn time were the same as the Mars-based system, the mass of the Earth-based mission would go to infinity. In
Table 8.2
the mass numbers are for the total mission. It is clear that the total launch requirement would probably be divided up into many launch vehicles.

You can see that the launch burden for sending the cargo to Ceres is about
50 times
less for missions starting ny than those departing from Earth, regardless of whether the technology employed is all chemical propulsion or chemical launch vehicles combined with nuclear electric propulsion for interplanetary transfer. If the launch vehicle used has a lift off mass of 1,000 tonnes, it would require 107 launches to assemble a methane/oxygen freighter mission launched from Earth, but only two launches for a departure from Mars. Even if propellant and other launch costs were 10 times greater on Mars than on Earth, it would still be enormously advantageous to launch from Mars. Furthermore, all this analysis assumes that the ships return from the asteroid belt without cargo. If the added burden of hauling enough propellant all the way out from Earth to return substantial amounts of asteroidal metal cargo without refueling at Mars is thrown into the mission requirement, then the Earth-based mission becomes even more hopeless.

The result that follows is simply this: Anything that needs to be sent to the asteroid belt that can be produced on Mars will be produced on Mars.

The outline of future interplanetary commerce thus becomes clear. There will be a “triangle trade,” with Earth supplying high-technology manufactured goods to Mars, Mars supplying low-technology manufactured goods and food staples to the asteroid belt and possibly to the Moon as well, and the asteroids sending metals (and perhaps the Moon sending helium-3) back to Earth. This triangle trade is directly analogous to the triangle trade of Britain, her North American colonies, and the West Indies during the colonial period. Britain would send manufactured goods to North America, the American colonies would send food staples and needed craft products to the West Indies, and the West Indies would send cash crops such as sugar to Britain. A similar triangle trade inv
olving Britain, Australia, and the Spice Islands also supported British trade in the East Indies during the nineteenth century.

POPULATING MARS

The difficulty of interplanetary travel may make Mars colonization seem visionary. However, colonization is, by definition, a one-way trip, and it is this fact that makes it possible to transport the large numbers of people that a colony in a new world needs to succeed.

Let us consider two models of how humans might emigrate to Mars: a government-sponsored model and a privately sponsored model.

If government sponsorship is available, the technological means required for immigration on a significant scale are essentially available today. In
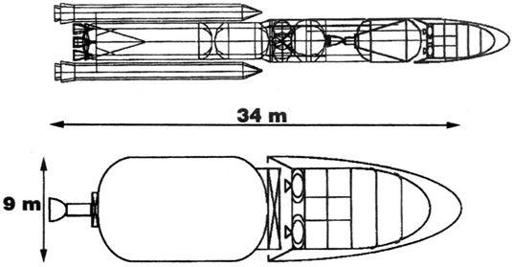
Figure 8.1
we see one version of such a concept that could be used to transport immigrants to Mars. A shuttle-derived heavy-lift launch vehicle lifts 145 tonnes (a Saturn V had about this same capacity) to low Earth orbit, then a nuclear thermal rocket (NTR, such as was demonstrated in the United States in the 1960s NERVA program) with an Isp of 900 seconds hurls a 70-tonne “habcraft” onto a seven-month trajectory to Mars. Arriving at Mars, the habcraft uses its conical aeroshell to aerobrake, and then parachutes and lands on its own sets of methane/oxygen engines.

The habcraft is 8 meters in diameter and includes four complete habitation decks, for a total living area of 200 square meters, allowing it to house 24 people adequately in space and on Mars. Expansion area is available in the fifth (uppermost) deck after the cargo it contains is unloaded upon arrival. Thus, in a single booster launch, 24 people, complete with their housing and tools, can be transported one way from Earth to Mars.

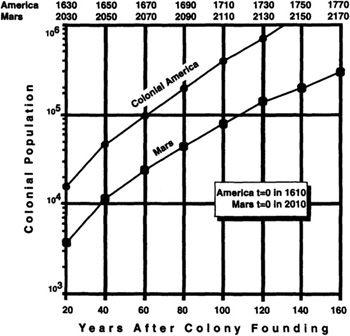
Now, let us assume for purposes of example that starting in10, an average of four such boosters are launched every year from Earth. If we then make various reasonable demographic assumptions, the population curve for Mars can be computed. The results are shown in
Figure 8.2
. Examining the graph, we see that with this level of effort (and the te
chnology frozen at late twentieth-century levels), the rate of human population growth of Mars in the twenty-first century would be about one-fifth that experienced by colonial America in the seventeenth and eighteenth centuries.

FIGURE 8.1
An NTR augmented heavy-lift launch vehicle, capable of transporting 24 colonists one-way to the Red Planet
.

This in itself is a very significant result. What it means is that the distance to Mars and the transportation challenge that it implies is not a major obstacle to the initiation of a human civilization on the Red Planet. Rather, the key questions, as discussed in Chapter 7, are those of resource utilization, growing food, building housing, and manufacturing all sorts of useful goods on the surface of Mars. Moreover the projected population growth rate, one-fifth that of colonial America, while a bit slow, is significant on a historical scale, and assuming a cost of $1 billion per launch, the $4 billion-per-year program cost could be sustained for some time by any major power on Earth that cared to plant the seeds of its posterity on Mars.

However, with a cost per launch of about $1 billion, the cost per immigrant would be $40 million. Such a price might be affordable to governments (for a time), but not to individuals or private groups. If Mars is ever to benefit from the dynamic energy of large numbers of immigrants motivated by personal choice seeking to make their mark in a new world, the transportation fee will have to drop a lot lower than this. Let us therefore examine an alternative model to see how low it is likely to drop.

FIGURE 8.2
Colonization of Mars compared to North America. Analysis assumes 100 immigrants per year starting in 2010, increasing at a 2 percent annual rate, 50/50 male/female. All immigrants are between ages 20 and 40. Average of 3.5 children to an ideal Martian family. Mortality rates are 0.1 percent per year between ages 0 and 59, 1 percent between ages 60 and 79, 10 percent per year for those over 80
.

Consider once again our methane/oxygen SSTO vehicles used to transport payloads from the surface of the Earth to low Earth orbit (LEO). For every kilogram of payload delivered to orbit, about 70 kilograms of propellant are required. Methane/oxygen bipropellant costs about $0.20/kilogram, so $14 of propellant costs will be incurred for every kilogram lifted to orbit. If we then assume total system operation cost is seven times propellant costs (roughly double the total cost/fuel cost ratio of airlines), then the cost of delivery to LEO could be about $100 per kilogram. Let’s assume that there is operating between Earth and Mars a spacecraft in a permanent cycling orbit which has the ability to recycle water and oxygen with 95 percent efficiency. Such interplanetary “cyclers,” proposed by Apollo 11 pilot Buzz Aldrin as the basis of a permanent Earth—Mars transportation system, could efficiently provide a
mple quarters for many immigrants, as they only have to be launched once but keep flying a 2.2-year round-trip journey between Earth and Mars virtually forever. Taking passage on such cyclers, each passenger (100 kilograms with personal effects) will have to bring about 400 kilograms of supplie to provide him or herself with food, water, and oxygen during a two-hundred-day outbound trip to Mars. Thus, 500 kilograms will need to be transported through a ΔV of about 4.3 km/s to move the immigrant from LEO to the cycling interplanetary spacecraft. The capsule used to transport the immigrant from LEO to the cycler and from the cycler to the Martian surface would probably need to have a mass of 500 kilograms per passenger. Thus, for each passenger a total of 1,000 kilograms needs to be delivered to the cycler orbit, which, with an Isp of 380 seconds for the methane/oxygen propulsion system on the transfer capsules, translates into 3,200 kilograms in LEO. At a delivery price of $100/kg to LEO, and assuming that the cost of the cycler itself is amortized over a very large number of missions, this in turn translates into a cost of $320,000 per passenger to Mars.

Obviously, I made a lot of assumptions in the above calculation that could be changed that would either raise or lower the calculated ticket price significantly. For example, use of air-breathing supersonic ramjet (“scramjet”) propulsion to perform a significant part of the Earth-to-orbit ΔV could cut orbit delivery costs by as much as a factor of three. An electric propulsion ferry could be used to lift the transfer capsule nearly to Earth escape, after which the capsule would be dropped to execute a powered flyby close to the Earth using high-thrust chemical stage. This would allow it to kick out of orbit and reach the cycler with a chemical ΔV of only 1.3 km/s, thereby doubling payload and reducing costs yet again. If the cycler employs a magnetic sail (see focus section) instead of simply using natural interplanetary orbits (with gravity assists), the hyperbolic velocity departing Earth required for cycler rendezvous can be essentially zero, thereby allowing the entire LEO-to-cycler delivery to be done by electric propulsion, or conceivably even solar or magnetic sails. Increasing the degree of closure of the life-support system on the cycler from our baseline of 95 percent of water and oxygen recycled to 99 percent would reduce the consumable delivery requ
irement for each passenger, thereby reducing passage costs still more. Thus, eventually Earth-to-Mars transportation costs could be expected to drop another order of magnitude, to $30,000 per passenger or so. The cost impacts as each of these innovations is progressively introduced are displayed in
Table 8.3
.