Structure and Interpretation of Computer Programs (97 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Exercise 5.19.
Alyssa P. Hacker wants a
breakpoint
feature in the simulator to
help her debug her machine designs. You have been hired to install
this feature for her. She wants to be able to specify a place in the
controller sequence where the simulator will stop and allow her to
examine the state of the machine. You are to implement a procedure
(set-breakpoint <
machine
> <
label
> <
n
>)
that sets a breakpoint just before the
n
th instruction after the
given label. For example,
(set-breakpoint gcd-machine 'test-b 4)
installs a breakpoint in
gcd-machine
just before the
assignment to register
a
. When the simulator reaches the
breakpoint it should print the label and the offset of the breakpoint
and stop executing instructions. Alyssa can then use
get-register-contents
and
set-register-contents!
to manipulate
the state of the simulated machine. She should then be able to
continue execution by saying
(proceed-machine <
machine
>)
She should also be able to remove a specific breakpoint by means of
(cancel-breakpoint <
machine
> <
label
> <
n
>)
or to remove all breakpoints by means of
(cancel-all-breakpoints <
machine
>)
4
Using the
receive
procedure here is a way to get
extract-labels
to effectively return two values –
labels
and
insts
– without explicitly making a compound data structure to
hold them. An alternative implementation, which returns an explicit
pair of values, is
(define (extract-labels text)
(if (null? text)
(cons '() '())
(let ((result (extract-labels (cdr text))))
(let ((insts (car result)) (labels (cdr result)))
(let ((next-inst (car text)))
(if (symbol? next-inst)
(cons insts
(cons (make-label-entry next-inst insts) labels))
(cons (cons (make-instruction next-inst) insts)
labels)))))))
which would be called by
assemble
as follows:
(define (assemble controller-text machine)
(let ((result (extract-labels controller-text)))
(let ((insts (car result)) (labels (cdr result)))
(update-insts! insts labels machine)
insts)))
You can consider our use of
receive
as demonstrating an elegant
way to return multiple values, or simply an excuse to show off a
programming trick. An argument like
receive
that is the next
procedure to be invoked is called a “continuation.” Recall that we
also used continuations to implement the backtracking control
structure in the
amb
evaluator in section
4.3.3
.
In section
5.4
, we will show how to implement a Scheme
evaluator as a register machine. In order to simplify the discussion,
we will assume that our register machines can be equipped with a
list-structured memory
, in which the basic operations for
manipulating list-structured data are primitive. Postulating the
existence of such a memory is a useful abstraction when one is
focusing on the mechanisms of control in a Scheme interpreter, but
this does not reflect a realistic view of the actual primitive data
operations of contemporary computers. To obtain a more complete
picture of how a Lisp system operates, we must investigate how list
structure can be represented in a way that is compatible with
conventional computer memories.
There are two considerations in implementing list structure. The
first is purely an issue of representation: how to represent the
“box-and-pointer” structure of Lisp pairs, using only the storage
and addressing capabilities of typical computer memories. The second
issue concerns the management of memory as a computation proceeds.
The operation of a Lisp system depends crucially on the ability to
continually create new data objects. These include objects that are
explicitly created by the Lisp procedures being interpreted as well
as structures created by the interpreter itself, such as environments
and argument lists. Although the constant creation of new data
objects would pose no problem on a computer with an infinite amount of
rapidly addressable memory, computer memories are available only in
finite sizes (more's the pity). Lisp systems
thus provide an
automatic storage allocation
facility to
support the illusion of an infinite memory. When a data object is no
longer needed, the memory allocated to it is automatically recycled
and used to construct new data objects. There are various
techniques for providing such automatic storage allocation. The
method we shall discuss in this section is called
garbage
collection
.
A conventional computer memory can be thought of as an array of
cubbyholes, each of which can contain a piece of information. Each
cubbyhole has a unique name, called its
address
or
location
. Typical memory systems provide two primitive operations:
one that fetches the data stored in a specified location and one that
assigns new data to a specified location. Memory addresses can be
incremented to support sequential access to some set of the
cubbyholes. More generally, many important data operations require
that memory addresses be treated as data, which can be stored in
memory locations and manipulated in machine registers. The
representation of list structure is one application of such
address arithmetic
.
To model computer memory, we use a new kind of data
structure called a
vector
. Abstractly, a vector is a compound
data object whose individual elements can be accessed by means of an
integer index in an amount of time that is independent of the
index.
5
In order to describe memory operations, we use two
primitive Scheme procedures for manipulating vectors:
- (vector-ref <
vector
> <
n
>)
returns the
n
th
element of the vector. - (vector-set! <
vector
> <
n
> <
value
>)
sets
the
n
th element of the vector to the designated value.
For example, if
v
is a vector, then
(vector-ref v 5)
gets
the fifth entry in the vector
v
and
(vector-set! v 5 7)
changes the value of the fifth entry of the vector
v
to 7.
6
For computer memory, this access can be implemented
through the use of address arithmetic to combine a
base address
that specifies the beginning location of a vector in memory with an
index
that specifies the offset of a particular element of the vector.
We can use vectors to implement the basic pair structures required for
a list-structured memory. Let us imagine that computer memory is
divided into two vectors:
the-cars
and
the-cdrs
. We will
represent list structure as follows: A pointer to a pair is an index
into the two vectors. The
car
of the pair is the entry in
the-cars
with the designated index, and the
cdr
of the pair is
the entry in
the-cdrs
with the designated index. We also need a
representation for objects other than pairs (such as numbers and
symbols) and a way to distinguish one kind of data from another.
There are many methods of accomplishing this, but they all reduce to
using
typed pointers
, that is, to extending the notion of
“pointer” to include information on data type.
7
The data type enables the system to
distinguish a pointer to a pair (which consists of the “pair” data
type and an index into the memory vectors) from pointers to other
kinds of data (which consist of some other data type and whatever is
being used to represent data of that type). Two data objects are
considered to be the same (
eq?
) if their pointers are
identical.
8
Figure
5.14
illustrates the use of this method to represent the list
((1 2) 3
4)
, whose box-and-pointer diagram is also shown. We use letter
prefixes to denote the data-type information. Thus, a pointer to the
pair with index 5 is denoted
p5
, the empty list is denoted by
the pointer
e0
, and a pointer to the number 4 is denoted
n4
. In the box-and-pointer diagram, we have indicated at the lower
left of each pair the vector index that specifies where the
car
and
cdr
of the pair are stored. The blank locations in
the-cars
and
the-cdrs
may contain parts of other list
structures (not of interest here).
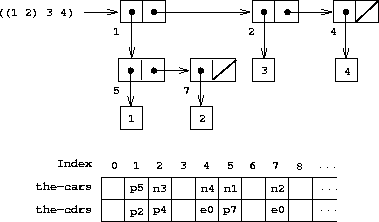 |
A pointer to a number, such as
n4
,
might consist of a type indicating numeric data together with the
actual representation of the number 4.
9
To deal with numbers that are too large to
be represented in the fixed amount of space allocated for a single
pointer, we could use a distinct
bignum
data type, for which the
pointer designates a list in which the parts of the number are
stored.
10
A symbol might be represented as a typed pointer that designates a
sequence of the characters that form the symbol's printed representation.
This sequence is constructed by the Lisp reader when the character string
is initially encountered in input. Since we want two instances of a
symbol to be recognized as the “same” symbol by
eq?
and we
want
eq?
to be a simple test for equality of pointers, we must
ensure that if the reader sees the same character string twice, it
will use the same pointer (to the same sequence of characters) to
represent both occurrences. To accomplish this, the reader maintains
a table, traditionally called the
obarray
, of all the symbols it
has ever encountered. When the reader encounters a character string
and is about to construct a symbol, it checks the obarray to see if it
has ever before seen the same character string. If it has not, it
uses the characters to construct a new symbol (a typed pointer to a
new character sequence) and enters this pointer in the obarray. If the
reader has seen the string before, it returns the symbol pointer
stored in the obarray. This process of replacing character strings by
unique pointers is called
interning
symbols.
Given the above representation scheme, we can replace each
“primitive” list operation of a register machine with one or more
primitive vector operations. We will use two registers,
the-cars
and
the-cdrs
, to identify the memory vectors, and will
assume that
vector-ref
and
vector-set!
are available as
primitive operations. We also assume that numeric operations on
pointers (such as incrementing a pointer, using a pair pointer to
index a vector, or adding two numbers) use only the index portion of
the typed pointer.
For example, we can make a register machine support the instructions
(assign <
reg
1
> (op car) (reg <
reg
2
>))
(assign <
reg
1
> (op cdr) (reg <
reg
2
>))
if we implement these, respectively, as
(assign <
reg
1
> (op vector-ref) (reg the-cars) (reg <
reg
2
>))
(assign <
reg
1
> (op vector-ref) (reg the-cdrs) (reg <
reg
2
>))
The instructions
(perform (op set-car!) (reg <
reg
1
>) (reg <
reg
2
>))
(perform (op set-cdr!) (reg <
reg
1
>) (reg <
reg
2
>))
are implemented as
(perform
(op vector-set!) (reg the-cars) (reg <
reg
1
>) (reg <
reg
2
>))
(perform
(op vector-set!) (reg the-cdrs) (reg <
reg
1
>) (reg <
reg
2
>))