Simply Complexity (22 page)

Anyone faced with designing a network, such as a road layout around a city, is faced with the following problem. Given that each mile of road costs a lot of money, to what extent do you trade off building more shortest paths through the central portion of the network – and hence potentially congesting the center – as opposed to enhancing decentralized pathways around the center, whose downside is that they may make journey times unnecessarily long, or become under-used? Tim Jarrett and Doug Ashton have looked in detail at this problem using a particularly neat mathematical theory to calculate the shortest journey times between any two points on the outer ring of a hub-and-spoke network. Their model correctly accounts for the competition between the following two issues concerning the number of spoke roads that should be built.

On the one hand, one might argue that adding more spoke roads will provide more shortest routes through the center, thereby shortening the average journey time. Hence the answer as to the optimum number of spoke roads to build is simply the maximum number that you can afford. This suggests that one should build as many spoke roads to the center as possible. But on the other hand, the more cars one allows to pass through the center, the more congested it will be. Hence the longer it will take to get from one side of the network to another. This suggests that one should build as few spoke roads to the center as possible.

Tim and Doug have proved mathematically that the competition between these two issues leads to an optimal number of
spoke roads that should be built, regardless of the fact that you might be able to afford more. In other words, by building not too many and not too few, the average journey time takes on its smallest value. This is summarized by the sketch in
figure 7.1
.

In addition to helping understand the interplay between centralized and decentralized flow on traffic networks, Tim and Doug’s research represents a fascinating yet novel approach to understanding how biological systems function by focusing on what actually happens on a network, as opposed to just analyzing the shape of the network structure itself. In other words, their work suggests that we should take a new look at biological systems in terms of costs and benefits of connections, rather than in terms of the physical structures themselves. Going back to the more mundane but no less important case of road traffic, their work gives us an important insight into how monetary charges should be levied on toll roads, according to the existing road structure. Their research also tells us something about how road layouts should be designed in order to achieve certain goals for journey times. For example, in the case of an existing hub-and-spoke traffic network, suppose there are 100 two-way roads passing through the center of the city and yet it turns out that having 50 is actually optimal. This could be achieved by
immediately converting them all to one-way roads such that 50 flow out and 50 flow in.

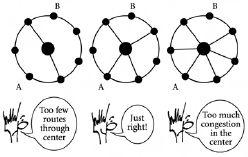
Figure 7.1
Take me to your center? The shortest average journey time is obtained by having neither too few, nor too many routes through the center.

But the most important practical application of their work is likely to be in determining what congestion charge should actually be levied – and more importantly, how. Let me explain what I mean by this. London currently charges a flat fee, regardless of how congested the center actually is when you drive through it. But why should it be a flat fee? Why shouldn’t the cost depend on how many other people are travelling through the city center at the same time as you? Indeed, this is an important conclusion of Tim and Doug’s work: they find that by varying the congestion cost according to how many other people are also driving through the center, the traffic can be optimized to coincide more closely with the actual number of access roads through the center – or indeed, the number that are actually operational at any given time. So this becomes much more like a market philosophy – instead of more buyers pushing the price up at that moment, more drivers passing through the center will push the congestion charge up at that moment.

The hub-and-spoke network is certainly of interest to most commuters – except if you live in a city like Houston which happens to have two ring-roads around the outside. In other words, Houston has an outer ring, a middle ring and a hub. In fact, there are many other everyday examples of such multiple-ring-and-hub structures: from biological systems through to corporate structures, administrative systems and communications systems. Consider, for example, the lines of communication in a typical hierarchical corporate structure as shown in figur
e 7.2
. It contains many levels of administration, with some connections between people in a given level and some connections between levels. Many readers may themselves already be working in such a structure – and so the question arises: if I want to get a message to someone within another layer, what route should I choose so that I have to involve as few people as possible? More generally, if we
were designing such a corporate ladder, what would be the design that leads to the quickest exchange of information between the most important layers? This could be important not only for corporations, but also for governments and military applications where decisions need to be transmitted between different layers of command as quickly as possible – or in situations where each additional contact represents an additional security risk.

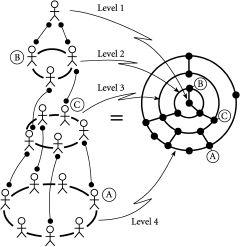
Figure 7.2
Lord of the Rings. A possible corporate, administrative, military or commercial structure of command. If a message needs to go quickly between A and B, and none of the levels is congested, the shortest route is via C. But what happens if level 3 gets too congested? Tim Jarrett and Doug Ashton’s mathematical theory helps provide an answer to such questions.

It would therefore be a fantastic breakthrough if one could extend Tim Jarrett and Doug Ashton’s mathematical theory to the more complex case of many interconnected rings rather than one. Remarkably, Tim and Doug have recently found a way of doing this for any number of rings. The trick is shown sketched in
figure 7.3
. By embedding one network in another, the hub-and-spoke of one network then becomes a new “super-hub” – or
so-called renormalized hub – for the larger, multiple-ring network. All that needs to be changed in the mathematical theory is to redefine the cost for going through the center, due to the fact that this renormalized hub now has a more complicated intrinsic structure than before. This renormalized hub can then be combined with other rings to form another renormalized hub which has an even more complicated intrinsic structure and hence a more general cost. Repeating this procedure over and over again, they can turn any multiple ring-and-hub network into a single ring-and-hub. So Houston – you don’t have a problem.

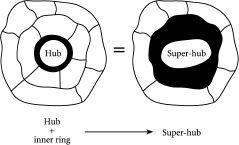
Figure 7.3
It’s a maze-ing. By redefining the cost for passing through the central hub, the problem of two rings can be turned into one ring. Repeating this process allows the reduction of a structure with any number of rings, down to a single ring problem which can then be solved using the mathematics developed by Tim Jarrett and Doug Ashton.

Thinking again about the construction of congestion charging schemes, one could therefore imagine having several different central zones – like rings within rings. So imagine that instead of a single central £8 zone in London, there could be two zones: one of £10 and one of £2. Or even better, the exact amounts could be adjusted in real-time, and announced on road-side electronic boards, in order to control the relative amounts of traffic in the two zones as the day progresses.

But Tim and Doug’s research has even deeper implications in terms of our understanding of biological systems. Teaming up with Mark Fricker’s group working on fungi, they have shown
that their theory offers an explanation as to why so many diverse sets of network structures arise in Nature under essentially the same environmental conditions. So let’s explore in more detail what they found and why it is so important. We mentioned earlier that there has been a lot of attention paid to the structure of the complex networks which are observed throughout the natural, biological and social sciences. The physics community, in particular, hopes that such networks might show particular universal properties. On the other hand, the biological community knows all too well that a wide diversity of structural forms can arise under very similar environmental conditions. In medicine, cancer tumors found growing in a given organ can have very different vascular networks. In plant biology, branching networks of plant roots or aerial shoots from different species can co-exist in very similar environments, yet look remarkably different in terms of their structure. Fungi provide a particularly good example – different species of fungi can form networks with varying degrees of lateral connections, and yet many exist under exactly the same environmental conditions. But given that such biological systems can adapt their structures over time in order to optimize their functional properties, why on earth do we observe such a wide variety of biological structures under essentially the same environmental conditions?

To answer this, we first need to know a bit about the eating habits of organisms such as a fungus. A primary functional property of an organism such as a fungus is to distribute nutrients efficiently around its network structure in order to survive. Suppose a fungus finds a lump of food somewhere on its perimeter. It needs to transport this food (carbon (C), nitrogen (N) and phosphorous (P)) across the structure to all other parts of the organism in order to feed itself. In the absence of any transport congestion effects, the average shortest path would be through the center; however, the fungus faces the possibility of food congestion in the central region since the tubes carrying the food do not have infinite capacity. Hence the organism must somehow decide how many pathways to build to the center in order to ensure nutrients get passed across the structure in a reasonably short time. In other words, the fungus – either in real-time or as a result of evolutionary
forces – chooses a particular connectivity to the central hub. But why should different fungi choose such different solutions under essentially the same environmental conditions? Which one is “right”? Tim, Doug and Mark’s work shows that, surprisingly, fungi with very different structures can all be right at the same time. More precisely, they have shown that very different network structures – such as those in
figure 7.4
– can share very similar values of the functional characteristics relevant to growth. In other words, the structures in
figure 7.4
can both be optimal in terms of transporting food. In particular, it takes the same amount of time in each structure to transport food from one side of the organism to the other.

An important further implication of their work is that in addition to searching for universality in terms of network structure, scientists should consider seeking universality in terms of network function – a message which is echoed by the results of David Smith’s fungus model in
chapter 5
. And in applications like cancer, the ability to say that two apparently quite different-looking tumors may – based on an analysis of the underlying vascular blood network – be identical and hence of equal malignancy, could prove to be an important breakthrough in terms of diagnosis.