Panic in Level 4: Cannibals, Killer Viruses, and Other Journeys to the Edge of Science (27 page)
Read Panic in Level 4: Cannibals, Killer Viruses, and Other Journeys to the Edge of Science Online
Authors: Richard Preston
Tags: #Richard Preston

“W
E THOUGHT TO OURSELVES
that it would be just a bit of number crunching,” Gregory said.
But, David said, “it wasn’t trivial.”
The brothers had a fairly easy time setting up the tiles on the Home Depot thing. When they tried to fit the puzzle together, however, they found that the pieces wouldn’t join properly; the warp and weft threads didn’t run smoothly from one tile to the next. The differences were vast. It was as if a tapestry had not been the same object from one moment to the next as it was being photographed. Sutures were visible. The result was a sort of Frankenstein version of the Unicorn Tapestries. The Chudnovskys had no idea why.
David, in exasperation, called up Barbara Bridgers. “Somebody has been fooling around with these numbers,” he told her.
“I don’t think so, David. Nobody around here could do that.”
David informed her that he and Gregory would need to obtain the complete set of raw data from the Leica camera. The next day, he went to the museum and collected, from Bridgers, two large blue Metropolitan Museum shopping bags stuffed with more than two hundred CDs, containing every number the Leica had collected from the Unicorn Tapestries. There were at least a hundred billion numbers in the shopping bags.
David took the subway back to Brooklyn, stopping off at a supermarket to buy some fruit. In the lab, he put his things down, and Gregory began going through them. “Where are the rest of the CDs?” he asked. One of the Metropolitan Museum bags was missing.
“My God! I left it on the subway,” David said. Half the Unicorn Tapestries could have been anywhere between the Upper Bronx and Far Rockaway.
They began frantically calling the subway’s lost and found. “Naturally, there was no answer,” Gregory recalled. David retraced his route. He found the Met bag sitting under the lettuce bin at the supermarket. Apart from being slightly misted, the CDs were okay.
Then the brothers really began to dig into the numbers. Working with Tom Morgan, they created something called a vector field, and they used it to analyze the inconsistencies in the images.
The tapestries, they realized, had changed shape as they were lying on the floor and being photographed. They had been hanging vertically for centuries; when they were placed on the floor, the warp threads relaxed. The tapestries began to breathe, expanding, contracting, shifting. It was as if, when the conservators removed the backing, the tapestries woke up. The threads twisted and rotated restlessly. Tiny changes in temperature and humidity in the room caused the tapestries to shrink or expand from hour to hour, from minute to minute. The gold-and silver-wrapped threads changed shape at different speeds and in different ways from the wool and silk threads.
“We found out that a tapestry is a three-dimensional structure,” Gregory went on. “It’s made from interlocked loops of wool.”
“The loops move and change,” David said.
“The tapestry is like water,” Gregory said. “Water has no permanent shape.”
The photographers had placed a thin sheet of gray paper below the edge of the part of the tapestry they were shooting. Each time they moved the camera, they also moved the sheet of paper. Though the paper was smooth and thin, it tugged the tapestry slightly as it moved, creating ripples. It stretched the weft threads and rotated the warp threads—it resonated through the tapestry. All this made the tiles impossible to join without the use of higher mathematics and the Home Depot thing.
A color digital photograph is composed of pixels. A pixel is the smallest picture element that contains color. The Unicorn Tapestries are themselves made up of the medieval equivalent of pixels—a single crossing of warp and weft is the smallest unit of color in the image. The woven pixels were maddening because they moved constantly. The brothers understood, at last, that it would be necessary to perform vast seas of calculations upon each individual pixel in order to make a complete image of a tapestry. Each pixel had to be calculated in its relationship to every other nearby pixel, a mathematical problem known as an N-problem, big enough to practically choke It. They decided to concentrate on just one of the tapestries, “The Unicorn in Captivity.” Gregory said, “This was a math problem similar to the analysis of DNA or speech recognition—”
“Look, my dear fellow, it was a real nightmare,” David said.
Two of the tiles on the front of “The Unicorn in Captivity” had an eerie green tinge. While the photographers were shooting them, someone had opened a door leading to the next room, where a fluorescent light was on, causing a subtle flare. The Chudnovskys corrected the lighting by using the color on the back threads as a reference. “It took us three months of computation,” Gregory said. “We should have just dropped it.”
The final assembly of the image took twenty-four hours inside the nodes of It, the Home Depot thing. Gregory and David stayed up all night and ran It from their respective apartments. In the preceding months, each pixel in “The Unicorn in Captivity” had been crunched through many billions of calculations. That last night, there were billions more calculations. By sunrise, the machine had recaptured “The Unicorn in Captivity” in its entirety. The image was flawless.
O
NE DAY IN AUTUMN
, my wife and our three children and I went to Brooklyn and paid a visit to the Chudnovskys at IMAS, which is in Rogers Hall, on the Polytechnic campus. David met us in the lobby. He wore a starched white shirt, dark slacks, and Hush Puppies. We were joined by Tom Morgan, a quiet man in his fifties with blue eyes, gold-rimmed spectacles, and a ponytail. He handed us disposable booties, of the kind worn by medical people in operating rooms. Then we went in.
The IMAS lab was a large, loftlike industrial room, with computer-controlled shades and lights, and filtered air. The lights were dim. The walls were concrete and painted white. The brothers projected images on the walls, and they also used the walls as a whiteboard to perform calculations with erasable markers. The walls were covered with scribbles—work in progress. Most of the floor consisted of a vast digital image, in color, showing 115 different equations arranged in a vast spiral that breaks up into waves near the walls—a whirlpool of mathematics.
The equations were a type known as a hypergeometric series. Among other things, they rapidly produce the digits of pi. The Chudnovskys discovered most of them; others were found by the great Indian mathematician Srinivasa Ramanujan, in the early twentieth century, and by Leonhard Euler, in the eighteenth century. On one corner of the floor there was a huge digital image of Albrecht Dürer’s engraving
Melencolia I.
In it, Melancholy is sitting lost in thought surrounded by various strange objects, including a magic square and a polyhedron with eight sides, called Dürer’s solid. The Chudnovskys suspected that Dürer’s solid is more curious mathematically than meets the eye.
Gregory Chudnovsky was half lying on the couch in his stocking feet, his body extended, facing the figure of Melancholy. His shoes, which were tucked inside surgical booties, had been left on the floor. He wore jeans and a soft leather jacket, and he seemed relaxed. Christine and Marian, who was five, were there. Marian was chattering and running around the lab happily. The effect of the child circling over her father’s swirling equations was slightly vertiginous.
“At first, we were going to cover the entire floor with
Melencolia,
but it made people dizzy,” Gregory said. “It made us dizzy, too. So we shrank it and moved it near the couch.”
Close to the windows stood the cluster of bare computers, sitting inside the frame of plumbing pipes and covered with window screens—It. There was a sound of many small whirring fans running inside It, keeping It cool. (I associate this sound with any room professionally occupied by the Chudnovskys.)

David and Gregory Chudnovsky in their laboratory at the Institute for Mathematics and Advanced Supercomputing (IMAS). The shadow profile behind them is that of Tom Morgan, their collaborator.
Dudley Reed
My daughter Marguerite, who was fifteen at the time, wanted to know which of the many equations in the floor was the one that the brothers had used to calculate pi with their previous supercomputer.
“Walk this way,” David said to her. “Now you are standing on the equation.”
She looked down. The equation swooped for a yard under her feet.
Because the Chudnovsky equation for pi is the most powerful and accurate formula for pi that’s ever been found, it is also the most nearly perfect representation of pi known to humanity, other than a symbol. Whether some hidden order exists in pi is still something unknown to humanity.
At the far end of the room hung two thirteen-foot-tall sheets of cloth, mounted at right angles to each other, that displayed perfect digital images of, respectively, the front and back of “The Unicorn in Captivity.” We walked up to the two pictures of the unicorn. First I looked at the front. I could see each thread clearly. The unicorn is spattered with droplets of red liquid that seems to be blood, although it may be pomegranate juice dripping from fruit in the tree. The threads in the droplets of blood are so deftly woven that they create an illusion that the blood is semitransparent. The white coat of the unicorn shines through.
Then I turned to the back of the tapestry. Here the droplets were a more intense red, with clearer highlights, and they seemed to jump out at the eye. The leaves of the flowers were a vibrant, plantlike green. (There are as many as twenty species of flowers in this tapestry. They are depicted with great scientific accuracy—greater than in any of the botany textbooks of the time. They include English bluebells, oxlip, bistort, cuckoopint, and Madonna lily. Botanists haven’t been able to identify a few; it’s possible that they are flowers that have gone extinct since 1500.) On the front, in contrast, the yellow dye in the green leaves has faded a bit, leaving them looking slightly bluish gray.
Gregory got up from the couch. David warned him to be careful, and he put his arm around Gregory’s waist, while Gregory leaned on David and put his arm over David’s shoulders. Then the Chudnovsky Mathematician moved slowly across the floor, until the brothers were standing (rather precariously) beside It. David explained that their image of the tapestry was a first step toward making even finer digital images of works of art. He said, “It’s simple to take a picture of a Vermeer, but what you really want is an image of the painting in 3-D, with a resolution better than fifty microns”—that’s about half the thickness of a human hair. “Then you can see the brushstrokes,” he went on, raising his voice over the whirring of the fans inside It. “You can catalog the brushstrokes in the sequence they occurred, as they were laid down on top of one another.”
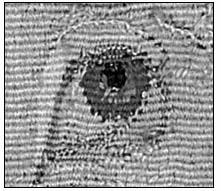
The eye of the unicorn, in reverse, on the back side of the tapestry. Detail from “The Unicorn in Captivity,” South Netherlandish, ca. 1495–1505. Wool warp, wool, silk, silver, and gilt wefts; 12 ft. 1 in.
×
99 in. (368 cm.
×
251.5 cm.). The Metropolitan Museum of Art, gift of John D. Rockefeller, Jr., 1937 (37.80.6).
Image © Metropolitan Museum of Art
When mathematicians work, they engage in intensely serious play. They follow their curiosity into problems that interest them. After playing with the unicorn, the Chudnovskys moved on.
“What are you doing now?” I asked.
David told me that they were working with IBM to design what may be the world’s most powerful supercomputer. The machine, code-named C64, was being built for a United States government agency.