In the Beginning Was Information (12 page)

– According to Theorem 6, a coding system is required for compiling information, and this system should be able to identify uniquely all the relevant amino acids by means of a standard set of symbols which must remain constant.

– As required by Theorems 14, 17, and 19, for any piece of information, this information should involve precisely defined semantics, pragmatics, and apobetics.

– There must be a physical carrier able to store all the required information in the smallest possible space, according to Theorem 24.

The names of the 20 amino acids occurring in living beings and their internationally accepted three-letter abbreviations are listed in Figure 16 (e.g., Ala for alanine). It is noteworthy that exactly this code with four different letters is employed; these four letters are arranged in "words" of three letters each to uniquely identify an amino acid. Our next endeavor is to determine whether this system is optimal or not.

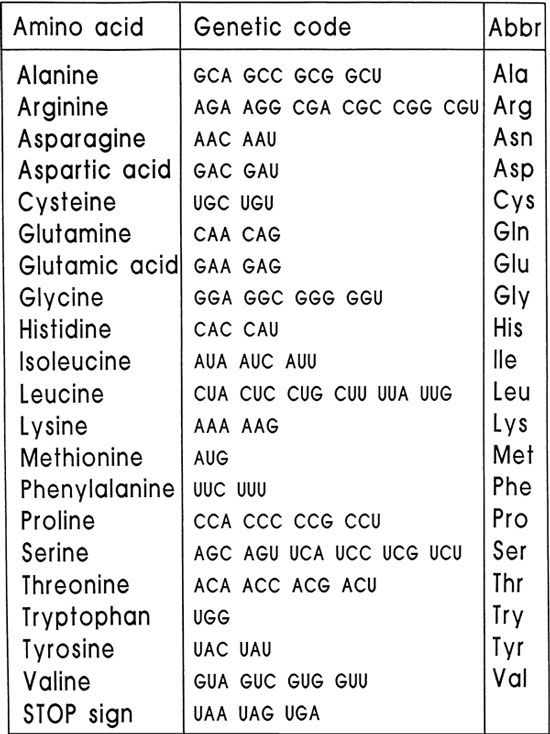Figure 16: The 20 amino acids which are present in living systems, given in alphabetic order, together with their international three-letter abbreviations. The code combinations (triplets) which give rise to the relevant acid are indicated in the right-hand column.

The storage medium is the DNA molecule (deoxyribonucleic acid), which resembles a double helix as illustrated in Figure 17. A DNA fiber is only about two millionths of a millimeter thick, so that it is barely visible with an electron microscope. The chemical letters A, G, T, and C are located on this information tape, and the amount of information is so immense in the case of human DNA that it would stretch from the North Pole to the equator if it was typed on paper, using standard letter sizes. The DNA is structured in such a way that it can be replicated every time a cell divides in two. Each of the two daughter cells must have identically the same genetic information after the division and copying processes. This replication is so precise, that it can be compared to 280 clerks copying the entire Bible sequentially each one from the previous one, with, at most, one single letter being transposed erroneously in the entire copying process.

Figure 17: The way in which genetic information is stored. At the left, the "chemical paper" is shown in the form of a long sugar-phosphate chain with the four chemical letters, A, T, C, and G. The actual structure and dimensions of a DNA molecule can be seen at the top.

When a DNA string is replicated, the double strand is unwound, and at the same time a complementary strand is constructed on each separate one, so that, eventually, there are two new double strands identical to the original one. As can be seen in Figure 17, A is complementary to T, and C to G.

One cell division lasts from 20 to 80 minutes, and during this time the entire molecular library, equivalent to one thousand books, is copied correctly.

Figure 18: The chemical formula of insulin. The A chain consists of 21 amino acids and the B chain is comprised of 30 amino acids. Three of the 20 amino acids present in living organisms, are absent (Asp, Met, Try), two occur six times (Cys, Leu), one five times (Glu), three occur four times (Gly, Tyr, Val), etc. The two chains are linked by two disulphide bridges. Insulin is an essential hormone, its main function being to maintain the normal sugar content of the blood at 3.9 to 6.4 mmol/l (70–115 mg/dl).

6.2 The Genetic Code

We now discuss the question of devising a suitable coding system. For instance, how many different letters are required and how long should the words be for optimal performance? If a certain coding system has been adopted, it should be strictly adhered to (theorem 8, par 4.2), since it must be in tune with extremely complex translation and implementation processes. The table in Figure 19 comprises only the most interesting 25 fields, but it can be extended indefinitely downward and to the right. Each field represents a specific method of encoding, for example, if n = 3 and L = 4, we have a ternary code with 3 different letters. In that case, a word for identifying an amino acid would have a length of L = 4, meaning that quartets of 4 letters represent one word. If we now want to select the best code, the following requirements should be met:

– The storage space in a cell must be a minimum, so that the code should economize on the required material. The more letters required for each amino acid, the more material is required, as well as more storage space.

– The copying mechanism described above requires n to be an even number. The replication of each of the two strands of DNA into complementary strands thus needs an alphabet having an even number of letters. For the purpose of limiting copying errors during the very many replication events, some redundance must be provided for (see appendix A 1.4).

– The longer the employed alphabet, the more complex the implementing mechanisms have to be. It would also require more material for storage, and the incidence of copying errors would increase.

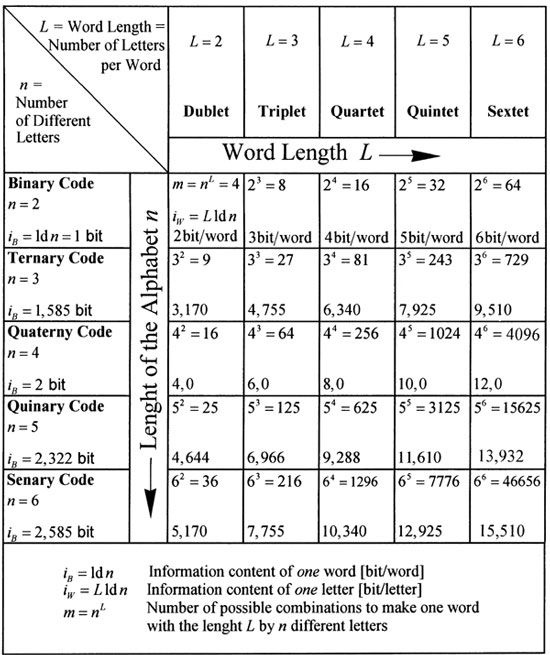Figure 19: The theoretical possibility of constructing a code consisting of words of equal length. Every field (block) represents a definite coding system as indicated by the number of different letters n, and the word length L.

In each field of Figure 19, the number of possible combinations for the different words appears in the top left corner. The 20 amino acids require at least 20 different possibilities and, according to Shannon’s theory, the required information content of each amino acid could be calculated as follows: For 20 amino acids, the average information content would be
i
_A
≡
i
_W
≡ ld 20 = log 20/log 2 = 4.32 bits per amino acid (ld is the logarithm with base 2).

If four letters (quartets) are represented in binary code (n = 2), then (4 letters per word)x(1 bit per letter) = 4 bits per word, which is less than the required 4.32 bits per word. This limit is indicated by the hatched boundary in Figure 19. The six fields adjacent to this line, numbered 1 to 6, are the best candidates. All other fields lying further to the right could also be considered, but they would require too much material for storage. So we only have to consider the six numbered cases.

It is, in principle, possible to use quintets of binary codes, resulting in an average of 5 bits per word, but the replication process requires an even number of symbols. We can thus exclude ternary code (n = 3) and quinary code (n = 5). The next candidate is binary code (No. 2), but it needs too much storage material in relation to No. 4 (a quaternary code using triplets), five symbols versus three implies a surplus of 67%. At this stage, we have only two remaining candidates out of the large number of possibilities, namely No. 4 and No. 6. And our choice falls on No. 4, which is a combination of triplets from a quaternary code having four different letters. Although No. 4 has the disadvantage of requiring 50% more material than No. 6, it has advantages which more than compensate for this disadvantage, namely:

– With six different symbols, the recognition and translation requirements become disproportionately much more complex than with four letters, and thus requires much more material for these purposes.

– In the case of No. 4, the information content of a word is 6 bits per word, as against 5.17 bits per word for No. 6. The resulting redundancy is thus greater, and this ensures greater accuracy for the transfer of information.

Conclusion: The coding system used for living beings is optimal from an engineering standpoint. This fact strengthens the argument that it was a case of purposeful design rather than fortuitous chance.

6.3 The Origin of Biological Information

We find a unique coding system and a definite syntax in every genome.
^[16]
The coding system is composed of four chemical symbols for the letters of the defined alphabet, and the syntax entails triplets representing certain amino acids. The genetic syntax system also uses structural units like expressors, repressors, and operators, and thus extends far beyond these two aspects (4 symbols and triplet words). It is not yet fully understood. It is known that the information in a cell goes through a cyclic process (Figure 20), but the semantics of this process is not (yet) understood in the case of human beings. The locations of many functions of chromosomes or genes are known, but we do not yet understand the genetic language. Because semantics is involved, it means that pragmatics also have to be fulfilled. The semantics are invariant, as can be seen in the similarity (not identity!) of uni-ovular twins. If one carefully considers living organisms in their entirety as well as in selected detail, the purposefulness is unmistakable. The apobetics aspect is thus obvious for anybody to see; this includes the observation that information never originates by chance, but is always conceived purposefully.

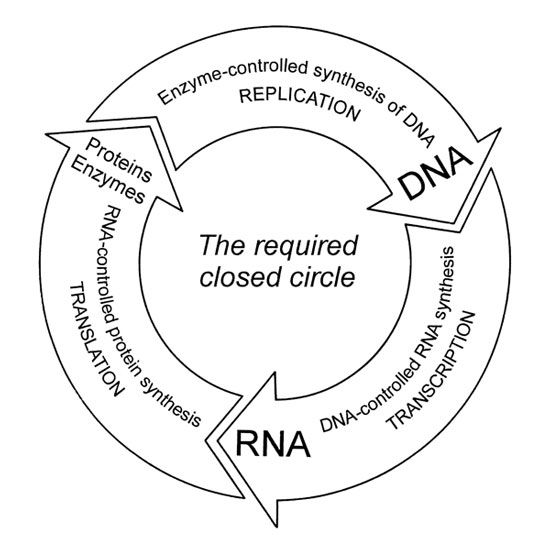Figure 20: A simplified representation of the cyclic information-controlled process occurring in living cells. The translation is based on pragmatics, but it is involved in the cyclic process of semantic information, since the DNA synthesis can only take place under enzymatic catalysis. This sketch clearly illustrates that such a cyclic process must have been complete right from the start, and could not have originated in a continuous process. The structure of this example of a complex information transfer system also corresponds to Figure 24.