Gödel, Escher, Bach: An Eternal Golden Braid (9 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

I gave you a theorem for free at the beginning, namely MI. Such "free" theorem is called an
axiom
-the technical meaning again being qui different from the usual meaning. A formal system may have zero, or several, or even infinitely many axioms. Examples of all these types v appear in the book.
Every formal system has symbol-shunting rules, such as the four rules of the
MIU
-
system. These rules are called either
rules of production
or
rules of inference
. I will use both terms.
The last term which I wish to introduce at this point is derivation. Shown below is a derivation of the theorem
MUIIU
:
(1)
MI
axiom
(2)
MII
from (1) by rule II
(3)
MIII
from (2) by rule II
(4)
MIIIIU
from (3) by rule I
(5)
MUIU
from (4) by rule III
(6)
MUIUUIU
from (5) by rule II
(7)
MUIIU
from (6) by rule IV
A derivation of a theorem is an explicit, line-by-line demonstration of how to produce that theorem according to the rules of the formal system. The concept of derivation is modeled on that of proof, but a derivation is an austere cousin of a proof. It would sound strange to say that you had
proven
MUIIU
, but it does not sound so strange to say you have
derived
MUIIU
.
Inside and Outside the System
Most people go about the MU-puzzle by deriving a number of theorems, quite at random, just to see what kind of thing turns up. Pretty soon, they begin to notice some properties of the theorems they have made; that is where human intelligence enters the picture. For instance, it was probably not obvious to you that all theorems would begin with
M
, until you had tried a few. Then, the pattern emerged, and not only could you see the pattern, but you could understand it by looking at the rules, which have the property that they make each new theorem inherit its first letter from an earlier theorem; ultimately, then, all theorems' first letters can be traced back to the first letter of the sole axiom
MI
-and that is a proof that theorems of the
MIU
-system must all begin with
M
.
There is something very significant about what has happened here. It shows one difference between people and machines. It would certainly be possible-in fact it would be very easy-to program a computer to generate theorem after theorem of the
MIU
-
system; and we could include in the program a command to stop only upon generating
U
.
You now know that a computer so programmed would never stop. And this does not amaze you. But what if you asked a friend to try to generate
U
? It would not surprise you if he came back after a while, complaining that he can't get rid of the initial
M
, and therefore it is a wild goose chase. Even if a person is not very bright, he still cannot help making some observations about what he is doing, and these observations give him good insight into the task-insight which the computer program, as we have described it, lacks.
Now let me be very explicit about what I meant by saying this shows a difference between people and machines. I meant that it is
possible
to program a machine to do a routine task in such a way that the machine will never notice even the most obvious facts about what it is doing; but it is inherent in human consciousness to notice some facts about the things one is doing. But you knew this all along. If you punch "1" into an adding machine, and then add 1 to it, and then add 1 again, and again, and again, and continue doing so for hours and hours, the machine will never learn to anticipate you, and do it itself, although any person would pick up the
pick up the idea, no matter how much or how well it is driven, that it i supposed to avoid other cars and obstacles on the road; and it will never learn even the most frequently traveled routes of its owner.
The difference, then, is that it is
possible
for a machine to act unobservant; it is impossible for a human to act unobservant. Notice I am not saying that all machines are necessarily incapable of making sophisticated observations; just that some machines are.
Nor am I saying that all people are always making sophisticated observations; people, in fact, are often very unobservant. But machines can be made to be totally unobservant; any people cannot. And in fact, most machines made so far are pretty close ti being totally unobservant. Probably for this reason, the property of being; unobservant seems to be the characteristic feature of machines, to most people. For example, if somebody says that some task is "mechanical", i does not mean that people are incapable of doing the task; it implies though, that only a machine could do it over and over without eve complaining, or feeling bored.
Jumping out of the System
It is an inherent property of intelligence that it can jump out of the tas which it is performing, and survey what it has done; it is always looking for and often finding, patterns. Now I said that an intelligence can jump out o its task, but that does not mean that it always will. However, a little prompting will often suffice. For example, a human being who is reading a boo may grow sleepy. Instead of continuing to read until the book is finished he is just as likely to put the book aside and turn off the light. He ha stepped
"out of the system" and yet it seems the most natural thing in the world to us. Or, suppose person
A
is watching television when person
B
comes in the room, and shows evident displeasure with the situation Person
A
may think he understands the problem, and try to remedy it b exiting the present system (that television program), and flipping the channel knob, looking for a better show. Person
B
may have a more radio concept of what it is to
"exit the system"-namely to turn the television oft Of course, there are cases where only a rare individual will have the vision to perceive a system which governs many peoples lives, a system which ha never before even been recognized as a system; then such people often devote their lives to convincing other people that the system really is there and that it ought to be exited from!
How well have computers been taught to jump out of the system? I w cite one example which surprised some observers. In a computer chess: tournament not long ago in Canada, one program-the weakest of all the competing ones-had the unusual feature of quitting long before the game was over. It was not a very good chess player, but it at least had the redeeming quality of being able to spot a hopeless position, and to resign then and there, instead of waiting for the other program to go through the boring ritual of checkmating. Although it lost every game it played, it did it in style. A lot of local chess experts were impressed. Thus, if you define "the system" as "making moves in a chess game", it is clear that this program had a sophisticated, preprogrammed ability to exit from the system. On the other hand, if you think of "the system" as being
"whatever the computer had been programmed to do", then there is no doubt that the computer had no ability whatsoever to exit from that system.
It is very important when studying formal systems to distinguish working
within
the system from making statements or observations
about
the system. I assume that you began the
MU
-puzzle, as do most people, by working within the system; and that you then gradually started getting anxious, and this anxiety finally built up to the point where without any need for further consideration, you exited from the system, trying to take stock of what you had produced, and wondering why it was that you had not succeeded in producing
MU
. Perhaps you found a reason why you could not produce
MU
; that is thinking about the system. Perhaps you produced
MIU
somewhere along the way; that is working within the system. Now I do not want to make it sound as if the two modes are entirely incompatible; I am sure that every human being is capable to some extent of working inside a system and simultaneously thinking about what he is doing. Actually, in human affairs, it is often next to impossible to break things neatly up into "inside the system" and "outside the system"; life is composed of so many interlocking and interwoven and often inconsistent "systems" that it may seem simplistic to think of things in those terms. But it is often important to formulate simple ideas very clearly so that one can use them as models in thinking about more complex ideas. And that is why I am showing you formal systems; and it is about time we went back to discussing the
MIU
-
system.
M-Mode, I-Mode, U-Mode
The MU-puzzle was stated in such a way that it encouraged some amount of exploration within the
MIU
-system-deriving theorems. But it was also stated in a way so as not to imply that staying inside the system would necessarily yield fruit. Therefore it encouraged some oscillation between the two modes of work. One way to separate these two modes would be to have two sheets of paper; on one sheet, you work "in your capacity as a machine", thus filling it with nothing but
M's
,
I
's, and
U
's; on the second sheet, you work "in your capacity as a thinking being", and are allowed to do whatever your intelligence suggests-which might involve using English, sketching ideas, working backwards, using shorthand (such as the letter `x'), compressing several steps into one, modifying the rules of the system to see what that gives, or whatever else you might dream up. One thing you might do is notice that the numbers 3 and 2 play an important role, since I's are gotten rid of in three's, and
U
's in two's-and doubling of length (except for the
M
) is allowed by rule II. So the second sheet might also have some figuring on it. We will occasionally refer back to these two modes of dealing with a formal system, and we will call them the
Mechanic mode (M-mode
) and the
Intelligent mode (I-mode
). To round out our mode with one for each letter of the
MIU
-system, I will also mention a fin mode-the
Un-mode (U-mode
), which is the Zen way of approaching thing. More about this in a few Chapters.
Decision Procedures
An observation about this puzzle is that it involves rules of two opposite tendencies-the
lengthening rules
and the
shortening rules
. Two rules (I and II) allow you to increase the size of strings (but only in very rigid, pr scribed ways, of course); and two others allow you to shrink strings somewhat (again in very rigid ways). There seems to be an endless variety to the order in which these different types of rules might be applied, and this gives hope that one way or another,
MU
could be produced. It might involve lengthening the string to some gigantic size, and then extracting piece after piece until only two symbols are left; or, worse yet, it might involve successive stages of lengthening and then shortening and then lengthening and then shortening, and so on. But there is no guarantee it. As a matter of fact, we already observed that
U
cannot be produced at all and it will make no difference if you lengthen and shorten till kingdom come.
Still, the case of
U
and the case of
MU
seem quite different. It is by very superficial feature of
U
that we recognize the impossibility of producing it: it doesn't begin with an M (whereas all theorems must). It is very convenient to have such a simple way to detect nontheorems. However who says that that test will detect
all
nontheorems?
There may be lots strings which begin with
M
but are not producible. Maybe
MU
is one of them. That would mean that the "first-letter test" is of limited usefulness able only to detect a portion of the nontheorems, but missing others. B there remains the possibility of some more elaborate test which discriminates perfectly between those strings which can be produced by the rules and those which cannot. Here we have to face the question,
"What do mean by a test?" It may not be obvious why that question makes sense, of important, in this context. But I will give an example of a "test" which somehow seems to violate the spirit of the word.
Imagine a genie who has all the time in the world, and who enjoys using it to produce theorems of the
MIU
-system, in a rather methodical way. Here, for instance, is a possible way the genie might go about it
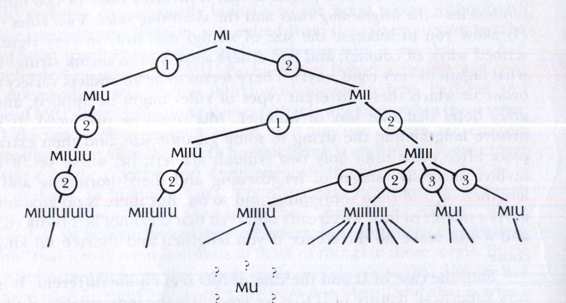
Step 1: Apply every applicable rule to the axiom MI. This yields two new theorems
MIU, MII.
Step 2: Apply every applicable rule to the theorems produced in step 1. This yields three new theorems:
MIIU, MIUIU, MIIII
.