Gödel, Escher, Bach: An Eternal Golden Braid (15 page)

There are beautiful alphabets which play with this figure-ground distinction. A message written in such an alphabet is shown below. At fir looks like a collection of somewhat random blobs, but if you step back ways and stare at it for a while, all of a sudden, you will see seven letters appear in this ..

.

FIGURE 15.

For a similar effect, take a look at my drawing
Smoke Signal
(Fig. 139). Along these lines, you might consider this puzzle: can you somehow create a drawing containing words in both the figure
and
the ground?

Let us now officially distinguish between two kinds of figures:
cursively
drawable
ones, and
recursive
ones (by the way, these are my own terms are not in common usage). A
cursively drawable
figure is one whose ground is merely an accidental by-product of the drawing act. A
recursive
figure is one whose ground can be seen as a figure in its own right. Usually this is quite deliberate on the part of the artist.

The "re" in "recursive" represents the fact that both foreground and background are cursively drawable – the figure is "twice-cursive". Each figure-ground boundary in a recursive figure is a double-edged sword. M. C. Escher was a master at drawing recursive figures-see, for instance, his beautiful recursive drawing of birds (Fig. 16).

FIGURE 16. Tiling of the plane using birds, by M. C. Escher (from a 1942 notebook).

Our distinction is not as rigorous as one in mathematics, for who can definitively say that a particular ground is not a figure? Once pointed out, almost any ground has interest of its own. In that sense, every figure is recursive. But that is not what I intended by the term. There is a natural and intuitive notion of recognizable forms. Are both the foreground and background recognizable forms? If so, then the drawing is recursive. If you look at the grounds of most line drawings, you will find them rather unrecognizable.

This demonstrates that

There exist recognizable forms whose negative space is not any recognizable form.

In more "technical" terminology, this becomes:

There exist cursively drawable figures which are not recursive.

Scott Kim's solution to the above puzzle, which I call his "FIGURE-FIGURE

Figure", is shown in Figure 17. If you read both black and white,

FIGURE 17. FIGURE-FIGURE Figure, by Scott E. Kim (1975).

you will see "FIGURE" everywhere, but "GROUND" nowhere! It is a paragon of recursive figures. In this clever drawing, there are two nonequivalent ways of characterizing the black regions:

(1) as the
negative space
to the white regions;

(2) as
altered copies
of the white regions (produced by coloring and shifting each white region).

(In the special case of the FIGURE-FIGURE Figure, the two characterizations are equivalent-but in most black-and-white pictures, they would not be.) Now in Chapter VIII, when we create our Typographical Number Theory (
TNT
), it will be our hope that the set of all false statements of number theory can be characterized in two analogous ways:

(1) as the negative space to the set of all
TNT
-theorems;

(2) as altered copies of the set of all
TNT
-theorems (produced by negating each
TNT
-theorem).

But this hope will be dashed, because:

(1) inside the set of all nontheorems are found some truths

(2) outside the set of all negated theorems are found some falsehoods

.

You will see why and how this happens, in Chapter XIV. Meanwhile, ponder over a pictorial representation of the situation (Fig. 18).

Figure and Ground in Music

One may also look for figures and grounds in music. One analogue is the distinction between melody and accompaniment-for the melody is always in the forefront of our attention, and the accompaniment is subsidiary, in some sense. Therefore it is surprising when we find, in the lower lines of a piece of music, recognizable melodies. This does not happen too often in post-baroque music. Usually the harmonies are not thought of as foreground. But in baroque music-in Bach above all-the distinct lines, whether high or low or in between, all act as "figures". In this sense, pieces by Bach can be called

"recursive".

Another figure-ground distinction exists in music: that between on-beat and off-beat. If you count notes in a measure "one-and, two-and, three-and, four-and", most melody-notes will come on numbers, not on "and"'s. But sometimes, a melody will be deliberately pushed onto the "and" 's, for the sheer effect of it. This occurs in several etudes for the piano by Chopin, for instance. It also occurs in Bach-particularly in his Sonatas and Partitas for unaccompanied violin, and his Suites for unaccompanied cello.

There, Bach manages to get two or more musical lines going simultaneously. Sometimes he does this by having the solo instrument play "double stops"-two notes at once. Other times, however, he

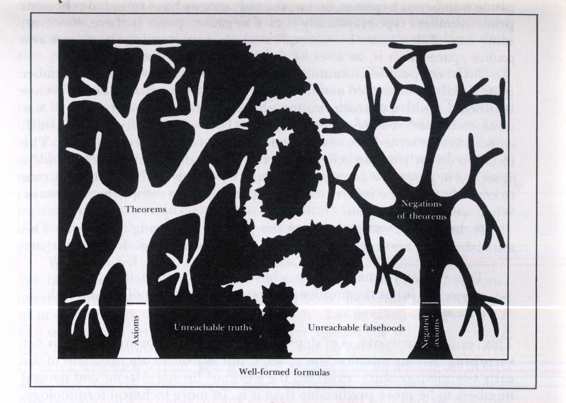
FIGURE 18. Considerable visual symbolism is featured in this diagram of the relation
between various classes of
TNT
strings. The biggest box represents the set of all
TNT

strings The next-biggest box represents the set of all well-formed TNT strings. Within it is
found~ set of all sentences of
TNT
. Now things begin to get interesting. The set of
theorems pictured as a tree growing out of a trunk (representing the set of axioms). The
tree-symbol chosen because of the recursive growth pattern which it exhibits: new
branches (theorems constantly sprouting from old ones. The fingerlike branches probe
into the corners of constraining region (the set of truths), yet can never fully occupy it.

The boundary beta the set of truths and the set of falsities is meant to suggest a randomly
meandering coastline which, no matter how closely you examine it, always has finer
levels of structure, an consequently impossible to describe exactly in any finite way. (See
B. Mandelbrot's book Fractals.) The reflected tree represents the set of negations of
theorems: all of them false yet unable collectively to span the space of false statements.

[Drawing by the author.]

puts one voice on the on-beats, and the other voice on the off-beats, so ear separates them and hears two distinct melodies weaving in and out, - harmonizing with each other.

Needless to say, Bach didn't stop at this level of complexity...

Recursively Enumerable Sets vs. Recursive Sets

Now let us carry back the notions of figure and ground to the domain formal systems. In our example, the role of positive space is played by
C
-type theorems, and the role of negative space is played by strings with a

prime number of hyphens. So far, the only way we have found to represent prime numbers typographically is as a negative space. Is there, however, some way-I don't care how complicated-of representing the primes as a
positive
space-that is, as a set of theorems of some formal system?

Different people's intuitions give different answers here. I remember quite vividly how puzzled and intrigued I was upon realizing the difference between a positive characterization and a negative characterization. I was quite convinced that not only the primes, but any set of numbers which could be represented negatively, could also be represented positively. The intuition underlying my belief is represented by the question:

"
How could a figure and its ground not carry exactly the same information
?" They seemed to me to embody the same information, just coded in two complementary ways.

What seems right to you?

It turns out I was right about the primes, but wrong in general. This astonished me, and continues to astonish me even today. It is a fact that:

There exist formal systems whose negative space (set of nontheorems) is not the positive space (set of theorems) of any formal system.

This result, it turns out, is of depth equal to Gödel’s Theorem-so it is not surprising that my intuition was upset. I, just like the mathematicians of the early twentieth century, expected the world of formal systems and natural numbers to be more predictable than it is. In more technical terminology, this becomes: There exist recursively enumerable sets which are not recursive.

The phrase
recursively enumerable
(often abbreviated "r.e.") is the mathematical counterpart to our artistic notion of "cursively drawable"-and
recursive
is the counterpart of "recursive". For a set of strings to be "r.e." means that it
can
be generated according to typographical rules-for example, the set of
C
-type theorems, the set of theorems of the
MIU
-system-indeed, the set of theorems of any formal system. This could be compared with the conception of a "figure" as "a set of lines which can be generated according to artistic rules" (whatever that might mean!). And a "recursive set" is like a figure whose ground is also a figure-not only is it r.e., but its complement is also r.e.

It follows from the above result that:

There exist formal systems for which there is no typographical decision procedure.

How does this follow? Very simply. A typographical decision procedure is a method which tells theorems from nontheorems. The existence of such a test allows us to generate all nontheorems systematically, simply by going down a list of
all
strings and performing the test on them one at a time, discarding ill-formed strings and theorems along the way. This amounts to

a typographical method for generating the set of nontheorems. But according to the earlier statement (which we here accept on faith), for
some
systems this is not possible.

So we must conclude that typographical decision procedures do not exist for all formal systems.

Suppose we found a set F of natural numbers (`
F
' for `Figure') whi4 we could generate in some formal way-like the composite numbers. Suppose its complement is the set G (for 'Ground')-like the primes. Together F and G make up all the natural numbers, and we know a rule for making all the numbers in set F, but we know no such rule for making all tl numbers in set G. It is important to understand that if the members of were always generated in order of
increasing
size
, then we could always characterize G. The problem is that many r.e. sets are generated I methods which throw in elements in an arbitrary order, so you never know if a number which has been skipped over for a long time will get included you just wait a little longer.