Games and Mathematics (42 page)
Read Games and Mathematics Online
Authors: David Wells

Visual versus verbal: geometry versus algebra
Women, games and mathematics
Mathematics and abstract games: an intimate connection


Another striking stylistic difference is between a preference for the visual or verbal. Bourbaki were very verbal. Felix Klein was very visual, and insisted that his students make models:
[Klein] had a strong power of geometric visualization, and all his investigations were essentially governed by appropriate geometric pictures…if you look at the drawings in his papers on automorphic functions, you will be astonished by the beauty of these figures, most of which are made up of very simple basic figures like triangles with curved sides. This beauty rests precisely on the fact that these figures illustrate the underlying mathematical relationships in an extremely simple and transparent way. Since Klein builds on these figures, all the results he derives possess that self-evidence which, as we said before, is the goal of mathematical research.
Twenty years ago, Ian Stewart wrote in
New Scientist
that,
New Scientist
that,
Attitudes to mathematics are changing; austere and formal pedantry is once more giving way to
ideas
, and it is becoming increasingly permissible to draw
pictures
that help to explain those ideas…Geometric thinking is back in vogue these days, though not in our schools. A month ago I was talking to an American mathematician who predicted a revival of geometry, resulting from the massive effort in computer graphics.
Mandelbrot would no doubt agree. He records how he one day sat in school as his teacher explained a problem, algebraically.
Mandelbrot's hand shot up, ‘Sir, you don't need to make any calculations. The answer is obvious.’ He described a geometrical approach that yielded a fast, simple solution. Where others would have used a formula, he saw a picture. The teacher, skeptical at first, checked. Correct. And Mandelbrot kept doing the same thing, in problem after problem, in class after class.
Mandelbrot has a very visual way of thinking: ‘I would say to myself: This construction is ugly, let's make it nicer. Let's make it symmetric. Let's project it. Let's embed it. And all that, I could see in perfect 3-D vision. Lines, planes, complicated shapes’ [Mandelbrot
2006
]. His work has subsequently been as far from pure abstraction as you can get:
2006
]. His work has subsequently been as far from pure abstraction as you can get:
Indeed, my work is unabashedly dominated by awareness of the importance of the messages of our senses. Fractal geometry is best identified in the study of the notion of roughness. More specifically, it allows a place of honour to full-fledged pictures that are as detailed as possible and go well beyond mere sketches and diagrams…But those pictures then went on to help me and many others generate new ideas and theories. Many of these pictures strike everyone as being of exceptional and totally unexpected beauty…In front of our eyes, the visual geometric intuition built on the practice of Euclid and of calculus is being retrained with the help of new technology.
So, contrary to the impression that pupils might get from their school textbooks, mathematicians do not all think in the same way and we might even say that mathematics is more than just ‘one’ subject, mathematicians’ styles of thinking being so extremely varied.
No one can fail to notice that most mathematicians and chess players – including almost all the greatest – have been men. Not only do few women reach the
heights of either profession, but fewer women choose to play on the lower slopes, as it were. Why? Part of the explanation must be an historical lack of opportunity for women but there may be other factors – such as style. We might hypothesise that many women have a distinct style of thinking compared to many men. Sherry Turkle and Seymour Papert have written that,
heights of either profession, but fewer women choose to play on the lower slopes, as it were. Why? Part of the explanation must be an historical lack of opportunity for women but there may be other factors – such as style. We might hypothesise that many women have a distinct style of thinking compared to many men. Sherry Turkle and Seymour Papert have written that,
When we looked closely at programmers in action we saw formal and abstract approaches; but we also saw highly successful programmers in relationships with their material that are more reminiscent of a painter than a logician. They use concrete and personal approaches to knowledge that are far from the cultural stereotypes of formal mathematics.
They then suggest that many women, more than men, are likely to think in such ways.
Several intellectual perspectives suggest that women would feel more comfortable with a relational, interactive, and connected approach to objects [in contrast to] men with a more distanced stance, planning, commanding, and imposing principles on them.
Turkle and Pappert imply both social and cognitive differences. Since women are generally more field-dependent than men it may be important that, ‘field-dependent secondary students experienced more mathematics anxiety than did field-independent learners’ [Hadfield & Maddux
1988
].
1988
].
Academic studies of women, girls and maths typically focus on their confidence, or fear of success, on learned helplessness, or whether mathematics is seen as useful, plus, invariably, differences in spatial ability, which do show up though the situation is far more complex than the naive claim that, ‘Men visualise better than women!’ [Fennema & Leder
1990
].
1990
].
Let's approach the question from the other side: what is special about male mathematicians? They typically appear competitive, very ambitious and driven. Reuben Fine, a one-time challenger for the world chess championship who retired from chess to become a psychoanalyst, and Benjamin Fine, claim that the mathematician is a
healthy
narcissist for whom mathematical creativity is an effective defence against anxiety [Fine & Fine
1977
].
healthy
narcissist for whom mathematical creativity is an effective defence against anxiety [Fine & Fine
1977
].
Thanks for the compliment! It may well be that many (especially pure) mathematicians do find that mathematics is a
successful
psychological defence against anxiety or anomie. What could be more meaningful, beautiful, and yet self-contained (and isolating if that's what you want) than mathematics – apart from chess! That line of thought suggests that mathematics will be especially attractive to individuals with a certain style of psychological defence, which
could explain why some people are so attracted to chess, or mathematics, while others are repelled.
successful
psychological defence against anxiety or anomie. What could be more meaningful, beautiful, and yet self-contained (and isolating if that's what you want) than mathematics – apart from chess! That line of thought suggests that mathematics will be especially attractive to individuals with a certain style of psychological defence, which
could explain why some people are so attracted to chess, or mathematics, while others are repelled.
Abstract games are an extraordinary cultural phenomenon, and so is
the mathematics
, as was said until quite recently, meaning both pure mathematics and all its many applications. Yet they are both embedded, together with traditional puzzles and mathematical recreations, in an aspect of society that has been there from its very origins. Let's return to an old theme that also could not be more modern.
the mathematics
, as was said until quite recently, meaning both pure mathematics and all its many applications. Yet they are both embedded, together with traditional puzzles and mathematical recreations, in an aspect of society that has been there from its very origins. Let's return to an old theme that also could not be more modern.
Knots have been around from the dawn of civilisation, and earlier, since they can form naturally in the twisting of vines and creepers. The 5400-year-old Ice Man discovered in the Alps in 1991 was remarkably preserved with all his equipment, which included a leather quiver with fourteen arrow shafts, a belt-purse, leather clothing, and other items, all of them sewn or knotted [Turner & van de Griend
1996
: 34].
1996
: 34].
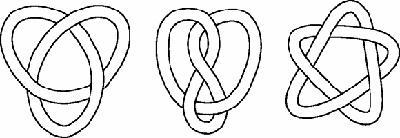
Figure 20.2
Three knots
with 3, 4 and 5 crossings
Three knots
with 3, 4 and 5 crossings

These drawings of the only knots with fewer than six crossings (
Figure 20.2
) already look
abstract
. Given a knot in a piece of string, you can copy it to another piece of string, or a rope, or even a ribbon or length of hair, because it is the
abstract
features that you copy, not the irrelevant details. Follow the rules – twist, put this end through the loop, push that loop through here, pull the other end through…and pull it tight – and the knot appears.
Figure 20.2
) already look
abstract
. Given a knot in a piece of string, you can copy it to another piece of string, or a rope, or even a ribbon or length of hair, because it is the
abstract
features that you copy, not the irrelevant details. Follow the rules – twist, put this end through the loop, push that loop through here, pull the other end through…and pull it tight – and the knot appears.
The rules for creating each knot are never arbitrary, nor are the rules for knitting or crocheting. As we have noted, there are only a limited number of basic types of knitting – or of tying a tie [Fink & Mao
2001
]. This fact is a pointer to the presence of mathematics behind these everyday activities.
2001
]. This fact is a pointer to the presence of mathematics behind these everyday activities.
Figure 20.3
Figure of ocean plait
Figure of ocean plait

The three stitches (
Figure 20.4
), taken from a Victorian book on sewing and sewing machines, are endless knots in a different sense. It is to be expected that knots can readily be created by machinery, repeating the same sequence of mechanical game-like moves as often as necessary.
Figure 20.4
), taken from a Victorian book on sewing and sewing machines, are endless knots in a different sense. It is to be expected that knots can readily be created by machinery, repeating the same sequence of mechanical game-like moves as often as necessary.
Figure 20.4
Three machine stitches from Victorian book
Three machine stitches from Victorian book

Knots and stitches, knitting and crochet, braids and weaving – and string figures – all display a hidden side of traditional culture. They can all be analysed mathematically – and they have been recently – yet for thousands of years they were not seen as mathematics but simply passed on (and changed and developed – new knots are still occasionally discovered) from one generation to the next.
Knots have long been puzzling. Alexander was challenged to undo the Gordian knot – he famously ‘solved’ the puzzle by cutting it. He was obviously a poor mathematician. The great physicist Paul Dirac was smarter. One day, observing a colleague's wife knitting, he realised that there was a second way to form the stitches, which he then proceeded to explain to the astonished woman. He had re-invented
purl and plain
.
purl and plain
.
Gauss sketched several knots
in his notebooks for 1794, and wrote a paper on electrodynamics which involved linked wires in space. His pupil Johann Listing wrote in 1847 the first book on
Topology
, in which discussed the theory of knots. [Turner and van de Griend
1996
: x, 262] They are now exploited by chemists, molecular biologists and physicists as well as mathematicians.
in his notebooks for 1794, and wrote a paper on electrodynamics which involved linked wires in space. His pupil Johann Listing wrote in 1847 the first book on
Topology
, in which discussed the theory of knots. [Turner and van de Griend
1996
: x, 262] They are now exploited by chemists, molecular biologists and physicists as well as mathematicians.
The latest apparition in the rarefied regions of modern cosmology is a competitor to string theory called loop quantum gravity in which space time is a network of abstract links and elementary particles are
braids
in this fabric. Who would have thought that a schoolgirl's plaits could be linked to the microstructure of the universe [Castelvecchi
2006
]?
braids
in this fabric. Who would have thought that a schoolgirl's plaits could be linked to the microstructure of the universe [Castelvecchi
2006
]?
Other books
The Highlander Takes a Bride by Lynsay Sands
On the Run by John D. MacDonald
The Nightlife: Paris (The Nightlife Series) by Travis Luedke
Between Worlds (Pendant Series Book 3) by Austin, Cynthia
Intimate Strangers by Denise Mathews
The Lady and the Panda by Vicki Croke
Taffy Sinclair 009 - The Truth About Taffy Sinclair by Betsy Haynes
The Letters of T. S. Eliot, Volume 1: 1898-1922 by T. S. Eliot
The Wild Zone by Joy Fielding