Games and Mathematics (36 page)
Read Games and Mathematics Online
Authors: David Wells

What about another possible fly in the ointment? There might be two or more ways to define a number such that i
2
= −1. Let's suppose that there are two different square roots of −1 and that they obey all the usual rules. Call them i and j, so that i
2
= −1 and j
2
= −1.
2
= −1. Let's suppose that there are two different square roots of −1 and that they obey all the usual rules. Call them i and j, so that i
2
= −1 and j
2
= −1.
Then i
2
− j
2
= 0 so, factoring, (i − j)(i + j) = 0.
2
− j
2
= 0 so, factoring, (i − j)(i + j) = 0.
So either i − j = 0 and i = j, or i + j = 0 and i = −j.
The first possibility is that there is only one root of −1. The second tells us that if i is a root then so is −i, but that's OK because we already know that, for example, 4 has two roots when negative numbers are included, +2 and −2. So if i
2
= −1 then we expect that (−i)
2
= −1 also. Going back to the usual identity,
 if i =
if i =
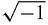 , so i
, so i
2
= −1 then,
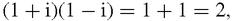 which certainly is strange, because 2 is usually thought of as a prime number, but if we introduce
which certainly is strange, because 2 is usually thought of as a prime number, but if we introduce
 it seems to have integer factors after all! In the factor 1+i, 1 is an integer and i =
it seems to have integer factors after all! In the factor 1+i, 1 is an integer and i =
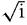 is a complex integer, so 1+i counts as a complex integer.
is a complex integer, so 1+i counts as a complex integer.
2
= −1 then we expect that (−i)
2
= −1 also. Going back to the usual identity,

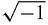 , so i
, so i2
= −1 then,
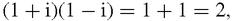
 it seems to have integer factors after all! In the factor 1+i, 1 is an integer and i =
it seems to have integer factors after all! In the factor 1+i, 1 is an integer and i =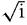 is a complex integer, so 1+i counts as a complex integer.
is a complex integer, so 1+i counts as a complex integer.So it seems that in order to accommodate this new discovery we shall have to change our idea of what an integer factor is, but this is not a serious problem to the mathematician. Changing definitions is something that mathematicians have often done as they explore their mathematical worlds more and more deeply.
Jean
Robert Argand (1768–1822) solved the problem of consistency by a method, then original, but now familiar: he built a model showing that complex numbers can be represented geometrically in the plane (Figure
18.3
).
Robert Argand (1768–1822) solved the problem of consistency by a method, then original, but now familiar: he built a model showing that complex numbers can be represented geometrically in the plane (Figure
18.3
).
Figure 18.3
Vertices of a rectangle in the complex plane
Vertices of a rectangle in the complex plane

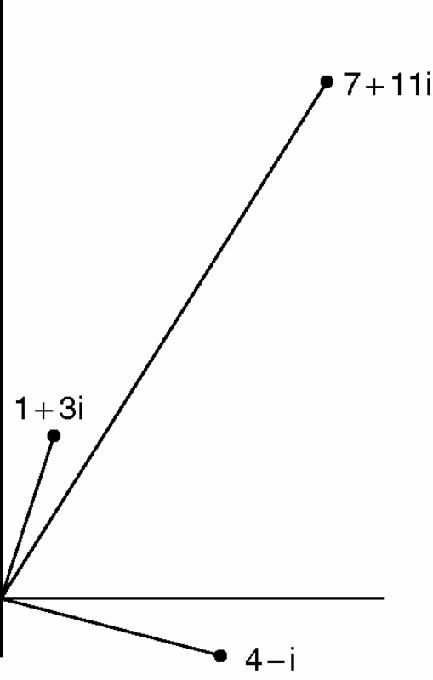
To the horizontal number line we add a vertical and independent complex number line. The graph shows the numbers 1 + 3i, 4 − i and their sum, 5 + 2i. Addition and subtraction become (to use modern language), the addition and subtraction of vectors but this poses no problems at all. Multiplication is more tricky but Argand can handle it. Each complex number, thought of as a vector, can be described by its length and the angle it makes with the real axis.
1+3i has length
 , by Pythagoras, and it makes an angle tan
, by Pythagoras, and it makes an angle tan
−1
3 or 71.565° with the real axis. 4 − i has length
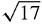 and angle −14.036° with the real axis.
and angle −14.036° with the real axis.
 , by Pythagoras, and it makes an angle tan
, by Pythagoras, and it makes an angle tan−1
3 or 71.565° with the real axis. 4 − i has length
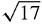 and angle −14.036° with the real axis.
and angle −14.036° with the real axis.We are now ready to calculate (1+3i)(4 − i) by algebra and by using Argand's diagram. By algebra, (1+3i)(4 − i) = 4+12i − i+3 = 7+11i which has length
 and makes an angle tan
and makes an angle tan
−1
11/7 or 57.529°.
 and makes an angle tan
and makes an angle tan−1
11/7 or 57.529°.
On Argand's diagram, we
multiply
the lengths and
add
the angles:
 ×
×
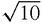 =
=
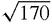 , and 71.565 − 14.036 = 57.529. The match is perfect, even allowing for errors in rounding off the three angles (Figure
, and 71.565 − 14.036 = 57.529. The match is perfect, even allowing for errors in rounding off the three angles (Figure
18.4
).
multiply
the lengths and
add
the angles:
 ×
×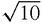 =
=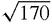 , and 71.565 − 14.036 = 57.529. The match is perfect, even allowing for errors in rounding off the three angles (Figure
, and 71.565 − 14.036 = 57.529. The match is perfect, even allowing for errors in rounding off the three angles (Figure18.4
).
Figure 18.4
Argand diagram showing product of two numbers
Argand diagram showing product of two numbers
Argand proved that the match is always perfect and it follows that elementary algebraic operations with complex numbers are equivalent to familiar operations with angles and similar triangles from Euclidean geometry and so we can indeed have complete confidence that if we add
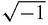 to everyday algebra we will not run into trouble.
to everyday algebra we will not run into trouble.
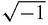 to everyday algebra we will not run into trouble.
to everyday algebra we will not run into trouble.Complex
numbers give us a new perspective on the very idea of a number, on the roots of equations, on the graphs which represent them, and so many other topics. Our next example is less powerful but it does show how apparently difficult problems can be almost miraculously solved by transformations that give us novel and powerful perspectives.
numbers give us a new perspective on the very idea of a number, on the roots of equations, on the graphs which represent them, and so many other topics. Our next example is less powerful but it does show how apparently difficult problems can be almost miraculously solved by transformations that give us novel and powerful perspectives.
Other books
The Adventures of Lazarus Gray by Barry Reese
One-Eyed Jack by Bear, Elizabeth
Confessions of a Werewolf Supermodel by Ronda Thompson
Where the Devil Can't Go by Lipska, Anya
Jack Carter and the Mafia Pigeon by Ted Lewis
Staying Strong: 365 Days a Year by Demi Lovato
Zeke and Ned by Larry McMurtry
Portrait in Sepia by Isabel Allende
Sweet Cry of Pleasure by Marie Medina
Angel by Elizabeth Taylor