Birth of a Theorem: A Mathematical Adventure (3 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

Lev Landau
With the physics of gases we are in the realm of Boltzmann: entropy increases, information is lost, the arrow of time points toward the future, the initial state is forgotten; gradually the statistical distribution of neutral particles approaches a state of maximum entropy, the most disordered state possible.
With plasma physics, on the other hand, we are in the realm of Vlasov: entropy is constant, information is conserved, there is no arrow of time, the initial state is always remembered; disorder does not increase, and there is no reason for the system to approach one state rather than another.
Landau had a low opinion of Vlasov, even going so far as to say that almost all of Vlasov’s results were wrong. And yet he adopted Vlasov’s model. Landau drew from it a conclusion that Vlasov had completely overlooked, namely, that the electrical forces weakened spontaneously over time without any corresponding increase in entropy or any friction whatsoever. Heresy?
Landau’s ingeniously complex mathematical calculation satisfied most physicists, and the so-called damping phenomenon soon came to be named after him. But not everyone was convinced.
Lyon
April 2, 2008
In the hallway, a low table strewn with pages of hastily scribbled notes and a blackboard covered with little drawings. Through the great picture window, a view of a gigantic long-legged black cubist spider, the famous P4 laboratory where experiments are conducted on the most dangerous viruses in the world.
My guest, Freddy Bouchet, gathered up his notes and put them in his bag. We’d spent a good hour talking about his research on the numerical simulation of galaxy formation and the mysterious power of stars to spontaneously organize themselves in stable clusters.

Freddy Bouchet
This phenomenon is not contemplated by Isaac Newton’s law of universal gravitation, discovered more than three hundred years ago. And yet when one observes a cluster of stars governed by Newton’s law, it does indeed seem that the entire cloud settles into a stable state after a rather long time—an impression that has been confirmed by a great many calculations performed on very powerful computers.
Is it possible, then, to
deduce
this property from the law of universal gravitation? The English astrophysicist Donald Lynden-Bell had no doubt whatsoever about the reality of dynamic stabilization in star clusters. He thought it was a “hard” phenomenon—as hard as, well, an iron meteorite—and gave it the name
violent relaxation
. A splendid oxymoron!
“Violent relaxation, Cédric, is like Landau damping. Except that Landau damping is a perturbative regime and violent relaxation is a highly nonlinear regime.”
Freddy was trained in both mathematics and physics, and he has devoted a good part of his professional life to studying such problems. Today he had come to talk to me about one question in particular.
“When you model galaxies, you treat the stars as a fluid—as a gas of stars, in effect. You go from the discrete to the continuous. But how great an error does this approximation entail? Does it depend on the number of stars? In a gas there are a billion billion particles, but in a galaxy there are only a hundred billion stars. How much of a difference does that make?”
Freddy went on in this vein for a long while, raising further questions, explaining recent results, drawing figures and diagrams on the board, noting references. I pointed out the connection between his research and one of my hobbyhorses, the theory of optimal transport inaugurated by Monge. Freddy seemed pleased; it was a profitable conversation for him. For my part, I was thrilled to see Landau damping suddenly make another appearance, scarcely more than a week after my discussion with Clément.
Just as I was coming back to my office after saying goodbye to Freddy, my neighbor Étienne, who until then had been bustling about, noiselessly filing papers, popped his head into the hallway. With his long gray hair cut in a bob, he looks like an elderly teenager, anticonformist but hardly threatening.
“I didn’t really want to say anything, Cédric, but those figures there on the board—I’ve seen them before.”
A plenary speaker at the last International Congress of Mathematicians, member of the French Academy of Sciences, often (and probably rightly) described as the world’s best lecturer on mathematics, Étienne Ghys is an institution unto himself. As a staunch advocate of promoting research outside the Paris region, he has spent the past twenty years developing the mathematics laboratory at ENS-Lyon. More than anyone else, he is responsible for turning it into one of the leading centers for geometry in the world. Étienne’s charisma is matched only by his grumpiness: he has something to say about everything—and nothing will stop him from saying it.

Étienne Ghys
“You’ve seen these figures?”
“Yes, that one’s from KAM theory. And this one, I know it from somewhere.…”
“Where should I look?”
“Well, KAM is found almost everywhere. You start from a completely integrable, quasi-periodic dynamic system and you introduce a small perturbation. There’s a problem with small divisors that eliminate certain trajectories, but even so, probabilistically speaking, you’ve got long-term stability.”
“Yes, I know. But what about the figures?”
“Hold on, I’m going to find a good book on the subject for you. But a lot of the figures you see in works on cosmology are usually found in dynamical systems theory.”
Very interesting, I’ll have to take a look. Maybe it will help me figure out what stabilization is really all about.
That’s what I love most of all about our small but very productive laboratory—the way conversation moves from one topic to another, especially when you’re talking with someone whose mathematical interests are different from yours. With no disciplinary barriers to get in the way, there are so many new paths to explore!
I didn’t have the patience to wait for Étienne to rummage through his vast collection of books, so I rooted around in my own library and came up with a monograph by Alinhac and Gérard on the Nash–Moser theorem. As it happens, I’d made a careful study of this work a few years ago, so I was well aware that the method developed by John Nash and Jürgen Moser is one of the pillars of the Kolmogorov–Arnold–Moser (KAM) theory that Étienne had mentioned. I also knew that Nash–Moser relies on Newton’s extraordinary iteration scheme for finding successively better approximations to the roots of real-valued equations—a method that converges unimaginably fast, exponentially exponentially fast!—and that Kolmogorov was able to exploit it with remarkable ingenuity. Frankly, I couldn’t see any connection whatever between these things and Landau damping. But who knows, I muttered to myself, perhaps Étienne’s intuition will turn out to be correct.…
Enough daydreaming! I wedged the book into my backpack and rushed off to pick up my kids from school, got on the métro and immediately took out a manga from my coat pocket. For a few brief and precious moments life around me disappeared, giving way to a world of supernaturally skilled physicians with surgically reconstructed faces, hardened yakuza who lay down their lives for their children, little girls with huge doe eyes, cruel monsters who suddenly turn into tragic heroes, little boys with blond curls who gradually turn into cruel monsters.… A skeptical and tender world, passionate, disillusioned, devoid of either prejudice or Manichaean certainties; a world of emotions that strike deep down in the soul and bring tears to the eyes of anyone innocent enough to surrender himself to them—
Hôtel de Ville! My stop! During the time it took to get here the story had flowed through my brain and through my veins, a small torrent of ink and paper. I felt cleansed through and through.
While I’m reading manga all thoughts of mathematics are suspended. It’s like hitting a pause button: manga and mathematics don’t mix. But what about later, when I’m dreaming at night? What if Landau, after the terrible accident that should have cost him his life, had been operated on by Black Jack? Surely the fiendishly gifted surgeon would have fully restored his powers, and Landau would have resumed his superhuman labors.…
For at least a brief time anyway, I was able to forget Étienne’s remark and this business about KAM theory. What connection could there possibly be between Kolmogorov and Landau? The moment I got off the métro, the question echoed through my mind over and over again. If there really is a connection, I’ll find it.
At the time I had no way of knowing that it would take me more than a year to find the link between the two. Nor could I have suspected the fantastic irony that would finally emerge: the figure that caught Étienne’s attention, that put him in mind of Kolmogorov, actually illustrates a situation where Landau damping and KAM theory have nothing to do with each other! Étienne’s intuition was right, but for the wrong reason—as though Darwin had guessed correctly about the evolution of species by comparing bats and pterodactyls, mistakenly supposing that the two were closely related.
Ten days after the unexpected turn taken by my working session with Clément, a second miraculous coincidence had occurred—and on the same subject! The timing could not have been more fortuitous.
Now to take advantage of it.
* * *
What was the name of that Russian physicist? Just like what happened to me, everyone thought he was dead when they pulled him out from the wreckage. Medically, he
was
dead. An extraordinary story. The Soviet authorities mobilized every resource in order to save an irreplaceable scientist. An appeal for help was even issued to physicians in other countries. The dead man was revived. For weeks the greatest surgeons in the world took turns at his bedside. Four times the man died. Four times life was artificially breathed into him. I’ve forgotten the details, but I do remember how fascinating it was to read about this struggle against an inadmissible fatality. His tomb was opened up and he was forcibly removed. He resumed his post at the university in Moscow.
[Paul Guimard,
Les choses de la vie
]
* * *
Newton’s law of universal gravitation states that any two bodies are attracted to each other by a force proportional to the product of their masses and inversely proportional to the square of the distance between them:
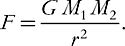
In its classical form, this law does a good job of accounting for the motion of stars in galaxies. But even if Newton’s law is simple, the immense number of stars in a galaxy makes it difficult to apply. After all, just because we understand the behavior of individual atoms doesn’t mean that we understand the behavior of a human being.…