Birth of a Theorem: A Mathematical Adventure (22 page)

From: Clement Mouhot

To: Cedric Villani

Subject: Landau version 51

I’m sending you what I’ve got, after going over everything line by line for 120 pages. I’m exhausted, going to take the night off. Here’s version 51, which should incorporate (having now carefully reviewed your messages) all your modifs and email requests (figures, remarks, dependence of constants…), as well as your rewritten section 10 (from the last version you sent me, version 50) and the new section 12.

For my part, I’ve reread everything up through section 9 (in other words up through page 118). There are a fair number of NdCMs that you’ll have to look at, but also a bunch of minor corrections that don’t seem to me to require any discussion. Only two of my comments raise concerns about the proofs (but in neither case do they call the result into question): section 7 page 100 and section 9 page 116.

Here’s what I suggest we do in the next couple days: how about if you work from this version 51 and go over sections 1 to 9, looking at all my comments and deleting each one in turn once you’ve dealt with it, in what let’s call version 51-cv, and I’ll carefully reread sections 10-11-12-13-14? (can we both aim to finish up by tomorrow evening or Wednesday morning?)

Best regards, Clement

TWENTY-SEVEN

Princeton

Morning of April 9, 2009

Uhhhhh … man, is it hard to wake up! Finally, with the greatest difficulty, I manage to sit up in bed.

Huh?

I hear a voice in my head.
You’ve got to bring over the second term from the other side, take the Fourier transform, and invert in
L
²
.

Unbelievable!

Scribble a note to myself on a scrap of paper, holler at the kids to get dressed, go down to make them breakfast. Hurry up or you’ll be late for school. Scampering out the door, skipping over the wet grass and beating me to the bus stop, they take their place in line behind the other children, patiently waiting to board a beautiful yellow-and-black bus—just like the ones in American movies!

Remarkable how many sons and daughters of top scientists take this bus to Littlebrook Elementary School every morning. Look, there are Ngô B
ả
o Châu’s kids! Ngô left Paris several years ago to accept a five-year visiting appointment at the IAS. He’s already famous in the mathematical community for his spectacular solution of a long-standing problem called the Fundamental Lemma, now being checked and verified. The branch of mathematics in which Ngô works, algebraic geometry, is renowned for its difficulty—and totally foreign to me. Everyone considers him an odds-on favorite for one of the next Fields Medals!

At Littlebrook the students are pampered. Private English lessons, instruction in other subjects tailored to their individual needs, etc. Great efforts are made to give them a sense of self-confidence—something American teachers can certainly be trusted to do. This afternoon the kids will come back from school in good spirits, actually looking forward to their homework. Lucky thing that the hatred of homework hasn’t yet reached the United States, at least not Princeton.

Once the kids are safely on their way I rush back home and settle down in an armchair to try out the idea that came to me when I woke up, as if by magic. Mumbling to myself all the while: “I stay in Fourier, as Sigal recommended, completely avoiding the Laplace transform. But before inverting, I begin by separating thus. Next, in a second step…”

I go on scribbling, then pause for a moment to reflect.

“It works! I think.…”

“YES! It works!!!
Of course
that’s the way you’ve got to do it, no question. We can elaborate later, add more details. But now the framework’s finally in place.”

From here on it’s only a matter of patience. Developing the idea will undoubtedly lead to schemes that I know what to do with. I write out the details carefully, taking my time. The moment has finally come to bring to bear all the ingenuity I can muster from eighteen years of doing mathematics!

“Hmmmm, now that resembles a Young inequality … and then it’s like proving Minkowski’s inequality … you change the variables, separate the integrals.…”

*   *   *

I went into semi-automatic pilot, drawing on the whole of my accumulated experience … but in order to be able to do this, first you’ve got to tap into a certain line—the famous direct line, the one that connects you to God, or at least the god of mathematics. Suddenly you hear a voice echoing in your head. It’s not the sort of thing that happens every day, I grant you. But it
does
happen.

I’d tapped into the direct line once before. In the winter of 2001, when I was teaching in Lyon, I lectured every Wednesday at the Institut Henri Poincaré in Paris. On one of those Wednesdays I was explaining my quasi-solution to Cercignani’s conjecture when Thierry Bodineau interrupted me and asked whether a certain part of the statement couldn’t be improved. Thinking about it on the high-speed train back to Lyon, the TGV, divine inspiration or something very much like it showed me the way to a much more powerful proof scheme, which made it possible to give a complete demonstration of the conjecture. Then, over the next few days, I was able to broaden the conjecture by extending the argument to cover a more general case.

But come the following Tuesday, just as I was about to proudly present my new results, I discovered a fatal error in the proof of the second theorem! I worked until three or four in the morning trying to fix it. No success.

Scarcely awake after only a few hours’ sleep, I began mulling over the problem again. I couldn’t bear the thought of not being able to announce my results. When I left home to go to the station, my head was filled with dead ends. But no sooner had I settled into my seat on the TGV than inspiration suddenly struck again: I
knew
what I had to do to fix the proof.

I spent the rest of the trip from Lyon to Paris putting everything in order, and when I entered the lecture hall I was able to keep my promise to myself after all. This made-in-TGV proof furnished the basis for one of my best articles only a few months later.

Now, once again, on this morning, the morning of April 9, 2009, another bit of inspiration came knocking at my brain’s door and illuminated everything!

Probably no one who read the article that finally appeared in
Acta Mathematica
had the least inkling of the euphoria I experienced that morning. Technique is the only thing that matters in a proof. It’s a pity there’s no place for the most important thing of all: illumination.

*   *   *

7.4.
Growth control.
To state the main result of this section we shall write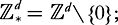
and if a sequence of functions
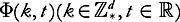is given, then
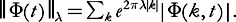We shall use
K
(s)
Φ
(t) as a shorthand for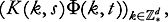
etc.

Theorem 7.7
(Growth control via integral inequalities).
Let f
⁰
=
f
⁰
(
v
) and
W
=
W
(
x
)
satisfy condition
(L)
from Subsection 2.2 with constants C
_0
,
λ
_0
,
κ
; in particular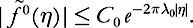
Let further