Bad Pharma: How Drug Companies Mislead Doctors and Harm Patients (29 page)

A new way of doing this is the subgroup analysis. The trick is simple: you’ve finished your trial, and it had a negative result. There was no difference in outcome – the patients on placebo did just as well as those on your new tablets. Your drug doesn’t work. This is bad news. But then you dig a little more, do some analyses, and find that the drug worked great for Hispanic non-smoking men aged fifty-five to seventy.

If it’s not immediately obvious why this is a problem, we have to go back and think about the random variation in the data in any trial. Let’s say your drug is supposed to prevent death during the duration of the trial. We know that death happens for all kinds of reasons, at often quite arbitrary moments, and is – cruelly – only partly predictable on the basis of what we know about how healthy people are. You’re hoping that when you run your trial, your drug will be able to defer some of these random unpredictable deaths (though not all, because no drug prevents all causes of death!), and that you’ll be able to pick up that change in death rate, if you have a sufficiently large number of people in your trial.

But if you go to your results after your trial has finished, and draw a line around a group of deaths that you can see, or around a group of people who survived, you can’t then pretend that this was an arbitrarily chosen subgroup.

If you’re still struggling to understand why this is problematic, think of a Christmas pudding with coins randomly distributed throughout it. You want to work out how many coins there are altogether, so you take a slice, a tenth of the pudding, at random, count the coins, multiply by ten, and you have an estimate of the total number of coins. That’s a sensible study, in which you took a sensible sample, blind to where the coins were. If you were to x-ray the pudding, you would see that there were some places in it where, simply through chance clumping, there were more coins than elsewhere. And if you were to carefully follow a very complex path with your knife, you would be able to carve out a piece of pudding with more coins in it than your initial sensible sample. If you multiply the coins in this new sample by ten, you will make it seem as if your pudding has lots more coins in it. But only because you cheated. The coins are still randomly distributed in the pudding. The slice you took after you x-rayed it and saw where the coins were is no longer informative about what’s really happening inside there.

And yet this kind of optimistic overanalysis is seen echoing out from business presentations, throughout the country, every day of the week. ‘You can see we did pretty poorly overall,’ they might say, ‘but interestingly our national advertising campaign caused a massive uptick in sales for lower-priced laptops in the Bognor region.’ If there was no prior reason to believe that Bognor is different from the rest of your shops, and no reason to believe that laptops are different from the rest of your products, then this is a spurious and unreasonable piece of cherry-picking.

More generally, we would say: if you’ve already seen your results, you can’t then find your hypothesis in them. A hypothesis has to come
before
you see the results which test it. So subgroup analyses, unless they’re specified before you begin, are just another way to increase your chances of getting a spurious, false positive result. But they are amazingly common, and amazingly seductive, because they feel superficially plausible.

This problem is so deep-rooted that it has been the subject of a whole series of comedy papers by research methodologists, desperate to explain their case to over-optimistic researchers who can’t see the flaws in what they’re doing. Thirty years ago, Lee and colleagues published the classic cautionary paper on this topic in the journal
Circulation
.
²⁷
They recruited 1,073 patients with coronary artery disease, and randomly allocated them to get either Treatment 1 or Treatment 2. Both treatments were non-existent, because this was a fake trial, a simulation of a trial. But the researchers followed up the real data on these real patients, to see what they could find, in the random noise of their progress.

They were not disappointed. Overall, as you would expect, there was no difference in survival between the two groups, since they were both treated the same way. But in a subgroup of 397 patients (characterised by ‘three-vessel disease’ and ‘abnormal left ventricular contraction’) the survival of Treatment 1 patients was significantly different from that of Treatment 2 patients, entirely through chance. So it turns out that you can show significant benefits, using a subgroup analysis, even in a fake trial, where both interventions consist of doing absolutely nothing whatsoever.

You can also find spurious subgroup effects in real trials, if you do a large enough number of spurious analyses.
²⁸
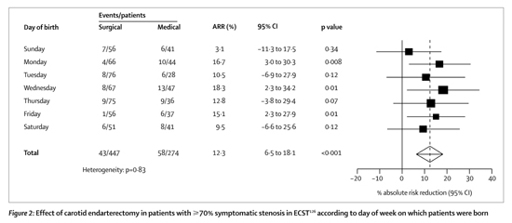
Researchers working on a trial into the efficacy of a surgical procedure called endarterectomy decided to see how far they could push this idea – for a joke – dividing the patients up into every imaginable subgroup, and examining the results. First they found that the benefit of the surgery depended on which day of the week the patient was born on (see below):
²⁹
if you base your clinical decisions on that, you’re an idiot. There was also a beautiful, almost linear relationship between month of birth and clinical outcome: patients born in May and June show a huge benefit, then as you move through the calendar there is less and less effect, until by March the intervention starts to seem almost harmful. If this finding had been for a biologically plausible variable, like age, that subgroup analysis would have been very hard to ignore.

Lastly, the ISIS-2 trial compared the benefits of giving aspirin or placebo for patients who’d just had a suspected heart attack. Aspirin was found to improve outcomes, but the researchers decided to do a subgroup analysis, just for fun. This revealed that while aspirin is very effective overall, it doesn’t work in patients born under the star signs of Libra and Gemini. Those two signs aren’t even adjacent to each other. Once again: if you chop up your data in lots of different ways, you can pull out lumpy subgroups with weird findings at will.

So should patients born under Libra and Gemini be deprived of treatment? You would say no, of course, and that would make you wiser than many in the medical profession: the CCSG trial found that aspirin was effective at preventing stroke and death in men, but not in women;
³⁰
as a result, women were under-treated for a decade, until further trials and overviews showed a benefit.

That is just one of many subgroup analyses that have misled us in medicine, often incorrectly identifying subgroups of people who wouldn’t benefit from a treatment that was usually effective. So, for example, we thought the hormone blocking drug tamoxifen was no good for treating breast cancer in women if they were younger than fifty (we were wrong). We thought clotbusting drugs were ineffective, or even harmful, when treating heart attacks in people who’d already had a heart attack (we were wrong). We thought drugs called ‘ACE inhibitors’ stopped reducing the death rate in heart failure patients if they were also on aspirin (we were wrong). Unusually, none of these findings was driven by financial avarice: they were driven by ambition, perhaps; excitement at new findings, certainly; ignorance of the risks of subgroup analysis; and, of course, chance.

Dodgy subgroups of trials, rather than patients

    You can draw a net around a group of trials, by selectively quoting them, and make a drug seem more effective than it really is. When you do this on one use of one drug, it’s obvious what you’re doing. But you can also do it within a whole clinical research programme, and create a confusion that nobody yet feels able to contain.

We’ve already seen that positive trials are more likely to be published and disseminated than negative ones, and that this can be misleading. Essentially, the problem is this: when we systematically review only the published trials, we are only seeing a subset of the results, and a subset that contains more positive results. We’ve taken a basket out with us to shop for trials, and been given only the nicest trials to put in it. But we’d be foolish to imagine that only nice trials exist.

This same problem – of how you take a sample of trials – can present itself in another, much more interesting way, best illustrated with an example.

Bevacizumab is expensive cancer drug – its sales in 2010 were $2.7 billion – but it doesn’t work very well. If you look on ClinicalTrials.gov, the register of trials (which has its own problems, of course) you will find about 1,000 trials of this drug, in lots of different kinds of cancer: from kidney and lung to breast and bowel, it’s being thrown at everything.

Inevitably – sadly – lots of results from these trials are missing. In 2010 two researchers from Greece set about tracking down all the studies they could find.
³¹
Looking only for the large ‘phase 3’ trials, where bevacizumab was compared against placebo, they found twenty-six that had finished. Of these, nine were published (representing 7,234 patients’ worth of data), and three had results presented at a conference (4,669 patients’ worth). But fourteen more trials, with 10,724 participating patients in total, remain unpublished.

That’s damnable, but it’s not the interesting bit.

They put all the results together, and overall it seems, regardless of which cancer you’re talking about, this drug gives a marginal, brief survival benefit, and to roughly the same extent in each kind of cancer (though remember, that’s before you take into account the side effects, and other very real costs). That’s not the interesting bit either: remember, we’re trying to get away from the idea that individual drug results are newsworthy, and focus on the structural issues, since they can affect every drug, and every disease.

This is the interesting bit. From June 2009 to March 2010, six different systematic reviews and meta-analyses on bevacizumab were published, each in a different type of cancer, each containing the few trials specific to that cancer.

Now, if any one of those meta-analyses reports a positive benefit for the drug, in one form of cancer, is that a real effect? Or is it a subgroup analysis, where there is an extra opportunity to get a positive benefit, regardless of the drug’s real effects, simply by chance, like rolling a dice over and over until you get a six? This is a close call. I think it’s a subgroup analysis, and John Ioannidis and Fotini Karassa, the two researchers who pulled this data together, think so too. None of the individual meta-analyses took into account the fact that they were part of a wider programme of research, with machine guns spraying bullets at a wall: at some stage, a few were bound to hit close together. Ioannidis and Karassa argue that we need to analyse whole clinical trials programmes, rather than individual studies, or clumps of studies, and account for the number of trials done with the drug on any disease. I think they’re probably right, but it’s a complicated business. As you can now see, there are traps everywhere.

‘Seeding Trials’

    Sometimes, trials aren’t really trials: they’re viral marketing projects, designed to get as many doctors prescribing the new drug as possible, with tiny numbers of participants from large numbers of clinics.

Let’s say you want to find out if your new pain drug, already shown to be effective in strict trials with ideal patients, also works in routine clinical use. Pain is common, so the obvious and practical approach is to use a small number of community clinics as research centres, and recruit lots of patients from each of these. Running your study this way brings many advantages: you can train a small number of participating doctors easily and cheaply; administrative costs will be lower; and you can monitor data standards properly, which means a better chance of good-quality data, and a reliable answer.

The ADVANTAGE trial on Vioxx was conducted very differently. They set out to recruit over 5,000 patients, but their design specified that each doctor should only treat a handful of patients. This meant that a vast number of participating doctors were required – six hundred by the end of the study. But that was OK for Merck, because the intention of this study wasn’t really to find out how good the drug was: it was to advertise Vioxx to as many doctors as possible, to get them familiar with prescribing it, and to get them talking about it to their friends and colleagues.

The basic ideas behind seeding trials have been discussed for many years in the medical literature, but only ever in hushed tones, with the threat of a defamation suit hanging over your head. This is because, even if the number of sites looks odd from the outside, you can’t be absolutely sure that any given project really is a seeding trial, unless you catch the company openly discussing that fact.

In 2008, new documents were released during unrelated litigation on Vioxx, and they produced exactly this proof.
³²
Although the ADVANTAGE trial was described to patients and doctors as a piece of research, in reality, reading the internal documents, it was intended as a marketing trial from the outset. One internal memo, for example, under the heading ‘description and rationale’, sets out how the trial was ‘designed and executed in the spirit of the Merck marketing principles’. Here these were, in order: to target a select group of critical customers (family doctors); to use the trial to demonstrate the value of the drug to the doctors; to integrate the research and marketing teams; and to track the number of prescriptions for Vioxx written by doctors after the trial finished. The data was handled entirely by Merck’s marketing division, and the lead author on the academic paper reporting the trial later told the
New York Times
that he had no role in either collecting or analysing the data.