Against the Gods: The Remarkable Story of Risk (47 page)

The example becomes more realistic when we translate it into a
technique for measuring the utility-the degree of satisfaction-of pos sessing $1 compared to the utility of possessing a second dollar, for a
total of $2. This man's favored outcome must now be $2, which takes
the place of milk in the above example; no money takes the place of
tea, the least favored outcome, and $1 becomes the middle choice and
takes the place of coffee.

Once again we ask our subject to choose between a sure thing and
a gamble. But in this case the choice is between $1 versus a gamble that
pays either $2 or nothing. We set the odds in the gamble at a 50%
chance of $2 and a 50% chance of nothing, giving it a mathematical
expectancy of $1. If the man declares that he is indifferent between the
$1 certain and the gamble, then he is neutral on the subject of risk at
this low level of the gamble. According to the formula proposed by von
Neumann and Morgenstern, the probability on the favorite possibilityin this case the $2 outcome-defines how much the subject prefers $1
over zero compared with how much he prefers $2 over zero. Here 50%
means that his preference for $1 over zero is half as great as his preference for $2 over zero. Under these circumstances, the utility of $2 is
double the utility of $1.

The response might well differ with other people or under other
circumstances. Let us see what happens when we increase the amount
of money involved and change the probabilities in the gamble. Assume
now that this man is indifferent between $100 certain and a gamble
with a 67% probability of paying $200 and a 33% probability of coming up zero. The mathematical expectancy of this gamble is $133; in
other words, the man's preference for the certain outcome-$100-is
now larger than it was when only a couple of dollars were involved.
The 67% probability on $200 means that his preference for $100 over
zero is two-thirds as great as his preference for $200 over zero: the utility of the first $100 is larger than the utility of the second $100. The
utility of the larger sum diminishes as the amount of money at risk
increases from single digits to triple digits.

If all this sounds familiar, it is. The reasoning here is precisely the
same as in the calculation of the "certainty equivalent," which we
derived from Bernoulli's fundamental principle that the utility of increases in wealth will be inversely related to the amount of wealth
already possessed (page 105). This is the essence of risk aversion-that
is, how far we are willing to go in making decisions that may provoke
others to make decisions that will have adverse consequences for us. This line of analysis puts von Neumann and Morgenstern strictly in the
classical mode of rationality, for rational people always understand their
preferences clearly, apply them consistently, and lay them out in the
fashion described here.

Alan Blinder, a long-time member of the Princeton economics faculty, co-author of a popular economics textbook, and Vice Chairman
of the Federal Reserve Board from 1994 to 1996, has provided an
interesting example of game theory.17 The example appeared in a paper
published in 1982. The subject was whether coordination is possible, or
even desirable, between monetary policy, which involves the control of
short-term interest rates and the supply of money, and fiscal policy,
which involves the balance between federal government spending and
tax revenue.

The players in this game are the monetary authorities of the Federal
Reserve System and the politicians who determine the mix between
government spending and tax revenues. The Federal Reserve authorities
perceive control of inflation as their primary responsibility, which makes
them favor economic contraction over economic expansion. They serve
long terms-fourteen years for members of the Board, and until retirement age for presidents of the Federal Reserve Banks-so they can act
with a good deal of independence from political pressures. The politicians, on the other hand, have to run regularly for election, which leads
them to favor economic expansion over economic contraction.

The object of the game is for one player to force the other to make
the unpleasant decisions. The Fed would prefer to have tax revenues
exceed spending rather than to have the government suffer a budget
deficit. A budget surplus would tend to hold inflation in check, thereby
protecting the members of the Fed from being seen as the bad guys.
The politicians, who worry about being elected, would prefer the Fed
to keep interest rates low and the money supply ample. That policy
would stimulate business activity and employment and would relieve
Congress and the President of the need to incur a budget deficit.
Neither side wants to do what the other side wants to do.

Blinder sets up a matrix that shows the preferences of each side in
regard to each of three decisions by the other: contract, do nothing, or expand. The numbers above the diagonal in each square represent the
order of preference of the members of the Fed; the numbers below the
diagonals represent the order of preference of the politicians.

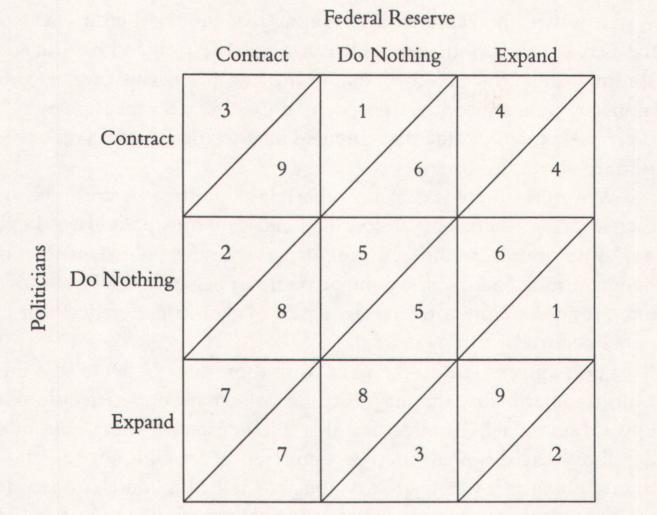
Blinder's payoff matrix.
(Adapted from Alan S. Blinder, 1982, "Issues in the Coordination of Monetary and
Fiscal Policies," in Monetary Policy Issues in the 1980s, Kansas City, Missouri:
Federal Reserve Bank of Kansas City, pp. 3-34.)

The highest-ranked preferences of the Fed (1, 2, and 3) appear in
the upper left-hand corner of the matrix, where at least one side is contractionary while the other is either supportive or does nothing to rock
the boat. The members of the Fed clearly prefer to have the politicians
do their job for them. The three highest-ranked preferences of the
politicians appear in the lower right-hand corner, where at least one
side is expansionary while the other is either supportive or does nothing to rock the boat. The politicians clearly prefer to have the Fed
adopt expansionary policies and for the politicians to do nothing. The
lowest-ranked preferences of the politicians appear in the left-hand column, while the lowest-ranked preferences of the Fed appear in the bottom row. This is hardly a situation in which much accommodation is
likely.

How will the game end? Assuming that the relationship between
the Fed and the politicians is such that collaboration and coordination
are impossible, the game will end in the lower left-hand corner where
monetary policy is contractionary and fiscal policy is expansionary. This
is precisely the outcome that emerged in the early Reagan years, when
Blinder wrote this paper.

Why this outcome and no other? First, both sides are displaying
their character here-an austere Fed and generous politicians. Under
our assumption that the Fed cannot persuade the politicians to run a
budget surplus and that the politicians cannot persuade the Fed to lower
interest rates, neither side has any desire to alter its preferences nor can
either dare to be simply neutral.

Look upward and to the right from those two 7s. Note that there
is no number below the diagonal (the politicians' preference) looking
upward on the left-hand vertical that is lower than 7; there is no number above the diagonal (the Fed's preference) looking horizontally to
the right that is lower than 7. As long as the Fed is contractionary and
the politicians are expansionary, both sides are making the best of a bad
bargain.

That is not the case in the upper right-hand corner, where the Fed's
monetary policy is less tight and a budget surplus emerges. Looking left
horizontally and above the diagonals, we note that both the choices rank
higher than 4: the Fed would rather do nothing or even be contractionary as compared to contributing to a business expansion that might
end up in an inflationary situation. The opposite view would prevail
among the politicians. Looking downward vertically, we find that both
the choices rank higher than 4: the politicians would rather do nothing
or run a deficit than follow a policy that cost them their jobs if their constituents lose their jobs as a result.

This outcome is known as a Nash Equilibrium, named after John
Nash, another Princetonian and one of the 1994 winners of the Nobel Prize for his contributions to game theory.18 Under the Nash
Equilibrium the outcome, though stable, is less than optimal. Both sides
would obviously prefer almost anything to this one. Yet they cannot
reach a better bargain unless they drop their adversarial positions and
work together on a common policy that would give each a supportive,
or at least a neutral, role that would keep them from getting into each
other's way. An example of that radically different state of affairs arose in 1994, when Fed policy was contractionary and the politicians were
uncharacteristically willing to stand by without interfering.

Blinder's game reveals a keen insight into the way contesting powers in Washington behave toward one another. But it can be generalized into many other situations: Drop the bomb, do nothing, or sue for
peace. Cut prices, do nothing, or raise prices. Bet your poker hand on
the basis of the probabilities, fold, or bluff.

In Blinder's example, the players know each other's intentions,
which is seldom the case. It also fails to include the preferences of consumers, employees, and business managers, all of whom are very much
involved in the outcome. When we change the rules by expanding the
number of players or by restricting the information available to the
players, we have no choice but to resort to higher mathematics. As
von Neumann and Morgenstern remarked, ". . . what a complexity of
theoretical forms must be expected in social theory."

In August 1993, the Federal Communications Commission decided
to auction off wireless communications rights. Two licenses would be
issued for each of 51 zones around the country; no bidder could acquire
more than one license in any zone. The usual procedure in such auctions is to call for sealed bids and to award the contract to the highest
bidders. This time, acting on the advice of Paul Milgrom, a Stanford
University professor, the FCC chose to conduct the auction according
to game theory, calling it a "Spectrum Auction."

First, all bids would be open, so that each contestant would always
know what all the others were doing. Second, there would be successive rounds of bidding until no contestant wanted to raise its bid any
higher. Third, between rounds, contestants could switch their bid from
one zone to another or could bid simultaneously for licenses in adjoining zones; since there is an economic advantage in having licenses in
adjoining zones, a particular license might be worth more to one party
than it would be to another. In short, each decision would be based on
the known decisions of the other players.

The contestants found that making decisions was no easy matter.
Each of them had to guess about the intentions of the others, studying
their reputation for aggressiveness, their financial capacity, and their existing licensing structures. On occasion, a properly placed bid by one
contestant would clearly signal its intentions to the others, thereby
avoiding a cycle of competitive bidding for some particular license.
Pacific Telesis, which hired Milgrom as their consultant in the auction,
went so far as to take out full-page ads in cities where potential competitors were located to make clear their determination to win no matter what. Some contestants joined together to prevent costly bidding
for the same license.