100 Essential Things You Didn't Know You Didn't Know (28 page)
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow

Can you prove it? Well, yes you can if you approach the question in the manner of many mathematical arguments. You start by assuming that the opposite is true and then use that assumption to deduce something that contradicts it. This means that your first assumption must have been false. It is an ultimate version of
the
gambit in chess wherein a player offers a piece to an opponent in the knowledge that, if it is taken, it opens the way for a much bigger gain in the future. It is the ultimate version of this manoeuvre because it is the whole game, rather than simply a single piece, that is being offered by this logical gambit.
Let us assume that there are uninteresting positive whole numbers and collect them together. If such a collection exists, then it will have a smallest member. But that smallest member is by definition interesting: it is the smallest uninteresting number. This contradicts our initial assumption that it is an uninteresting number. So our first assumption, that there are uninteresting numbers, was false. All numbers must be ‘interesting’.
Just to prove it, here is a story, well known among mathematicians, that is told about the English mathematician Godfrey Hardy when he went to visit his friend, the remarkable Indian mathematician Srinivasa Ramanujan, in a London hospital: ‘In the taxi from London, Hardy noticed its number, 1729. He must have thought about it a little because he entered the room where Ramanujan lay in bed and, with scarcely a hello, blurted out his disappointment with it. It was, he declared, “rather a dull number”, adding that he hoped that wasn’t a bad omen. “No, Hardy,” said Ramanujan, “it is a very interesting number. It is the smallest number expressible as the sum of two cubes in two different ways.”
fn1
Such numbers are now known as ‘taxicab’ numbers in memory of this incident.
fn1
Because 1729 = 1
3
+ 12
3
= 9
3
+ 10
3
. The cubes have to be positive in these examples. If you allow negative numbers to be cubed, then the smallest such number is 91 = 6
3
+ (-5)
3
= 4
3
+ 3
3
.
90
Incognito
The number you have reached does not exist.
Recorded message for unobtainable Italian phone numbers
fn1
In the sixteenth and seventeenth centuries it was not uncommon for the leading mathematicians of the day to publish their discoveries in code. This seems very strange to modern scientists, who clamour for recognition and priority in being the first to discover something, but there was some method to the seeming madness of those early mathematicians. They wanted to have their proverbial cake and eat it. Publishing a discovery that makes use of a new mathematical ‘trick’ establishes you as its discoverer, but it also reveals the trick so that others can use it and beat you to other, possibly greater, discoveries. You have a choice: hold off announcing the first discovery until you have given yourself time to investigate other possibilities more closely – and run the risk that someone else will discover and publish your first result – or you could publish an encoded version of your discovery. Assuming no one breaks the code, your new trick is safe from exploitation by others, and if anyone else comes along and announces they have discovered what you have already found, you can just apply the decrypt to show that you made the discovery long before. Very devious – and I hasten to add that such behaviour does not go on
today
in science and mathematics, and probably wouldn’t be tolerated if it was attempted. However, it does happen in the world of literature. Books like the political novel
Primary Colours
, about the Presidential election campaign of Bill Clinton, written by an initially unidentified journalist using a pseudonym, look a little like an attempt to have it both ways.
Suppose that you wanted to conceal your identity in a similar way today, how could you use simple maths to do it? Pick a couple of very large prime numbers, for example 104729 and 105037 (actually you want to pick much larger ones, with hundreds of digits, but these are big enough to get the general idea). Multiply them together to get the product: 11000419973. Incidentally, don’t trust your calculator, it probably can’t cope with such a large number and will round the answer off at some stage – my calculator gave the wrong answer 11000419970.
Now, let’s go back to our secret publishing challenge. You want to publish your discovery and not reveal your identity publicly, but include a hidden ‘signature’ so that at some future date you can show that you wrote it. You could publish the book with that huge product of two prime numbers, 11000419973, printed in it at the back. You know the two factors (104729 and 105037) and can easily multiply them together to show that the answer is your product ‘code’. However, if other people start with 11000419973, they will not find it so easy to find the two factors. If you had chosen to multiply together two very large prime numbers, each with 400 digits, then the task of finding the two factors could take a lifetime, even if assisted by a powerful computer. It is not impossible to break our ‘code’, but using much longer numbers is an unnecessary level of security – it just needs to take a very long time.
This operation of multiplying and factoring numbers is an example of a so-called ‘trapdoor’ operation (see
Chapter 27
). It’s quick and easy to go in one direction (like falling through a trapdoor), but longwinded and slow to go in the opposite direction
(like climbing back up through the trapdoor). A more complicated version of multiplying two prime numbers is used as the basis for most of the world’s commercial and military codes today. For example, when you buy anything online and enter your credit card details into a secure website, the details are compounded with large prime numbers, transmitted to the company and then decrypted by prime number factorisation.
fn1
In Italian: ‘Il numero selezionato da lei è inesistente.’
91
The Ice Skating Paradox
After finishing dinner, Sidney Morgenbesser decides to order dessert. The waitress tells him he has two choices: apple pie and blueberry pie. Sidney orders the apple pie. After a few minutes the waitress returns and says that they also have cherry pie, at which point Morgenbesser says, ‘In that case I’ll have the blueberry pie!’
Academic legend
When we make choices or cast votes, it seems rational to expect that, if we first chose K as the best among all the alternatives on offer, and then someone comes along and tells us that there is another alternative, Z, which they forgot to include, our new preferred choice will be to stick with K or to choose Z. Any other choice seems irrational because we would be choosing one of the options we rejected first time around in favour of K. How can the addition of the new option change the ranking of the others?
The requirement that this should not be allowed to happen is so engrained in the minds of most economists and mathematicians that it is generally excluded by fiat in the design of voting systems. Yet, we know that human psychology is rarely entirely rational and there are situations where the irrelevant alternative changes the order of our preferences, as it did with Sidney Morgenbesser’s pie order (of course, he could have seen one of the pies in question between orders).
A notorious example was a transport system that offered a red bus service as an alternative to the car. Approximately half of all travellers were soon found to use the red bus; half still used a car. A second bus, blue in colour, was introduced. We would expect one quarter of travellers to use the red bus, one quarter to use the blue bus, and one half to continue travelling by car. Why should they care about the colour of the bus? In fact, what happened was that one third used the red bus, one third the blue bus, and one third their car!
There is one infamous situation where the effect of irrelevant alternatives was actually built into a judging procedure, with results so bizarre that they eventually led to the abandonment of that judging process. The situation in question was the judging of ice skating performances at the Winter Olympics in 2002, which saw the young American Sarah Hughes defeat favourites Michelle Kwan and Irina Slutskaya. When you watch skating on the television the scores for an individual performance (6.0, 5.9, etc.) are announced with a great fanfare. However, curiously, those marks do not determine who wins. They are just used to order the skaters. You might have thought that the judges would just add up all the marks from the two programmes (short and long) performed by each individual skater, and the one with the highest score wins the gold medal. Unfortunately, it wasn’t like that in 2002 in Salt Lake City. At the end of the short programme the order of the first four skaters was:
Kwan (0.5), Slutskaya (1.0), Cohen (1.5), Hughes (2.0).
They are automatically given the marks 0.5, 1.0, 1.5 and 2.0 because they have taken the first four positions (the lowest score is best). Notice that all those wonderful 6.0s are just forgotten. It doesn’t matter by how much the leader beats the second place skater, she only gets a half-point advantage. Then, for the performance of the long programme, the same type of scoring system
operates
, with the only difference being that the marks are doubled, so the first placed skater is given score 1, second is given 2, third 3 and so on. The score from the two performances are then added together to give each skater’s total score. The lowest total wins the gold medal.
After Hughes, Kwan and Cohen had skated their long programmes Hughes was leading, and so had a long-programme score of 1, Kwan was second so had a score of 2, and Cohen lay third with a 3. Adding these together, we see that before Slutskaya skates the overall marks are:
1st: Kwan (2.5), 2nd: Hughes (3.0), 3rd: Cohen (4.5)
Finally, Slutskaya skates and is placed second in the long programme, so now the final scores awarded for the long programme are:
Hughes (1.0), Slutskaya (2.0), Kwan (3.0), Cohen (4.0).
The result is extraordinary: the overall winner is Hughes because the final scores are:
1st: Hughes (3.0), 2nd: Slutskaya (3.0), 3rd: Kwan (3.5), 4th: Cohen (5.5)
Hughes has been placed ahead of Slutskaya because, when the total scores are tied, the superior performance in the long programme is used to break the tie. But the effect of the poorly constructed rules is clear. The performance of Slutskaya results in the positions of Kwan and Hughes being changed. Kwan is ahead of Hughes after both of them have skated, but after Slutskaya skates Kwan finds herself behind Hughes! How can the relative merits of Kwan and Hughes depend on the performance of Slutskaya? The paradox of irrelevant alternatives rules ok.
92
The Rule of Two
History is just one damn thing after another.
Henry Ford
Infinities are tricky things and have perplexed mathematicians and philosophers for thousands of years. Sometimes the sum of a never-ending list of numbers will become infinitely large; sometimes it will get closer and closer to a definite number; sometimes it will defy having any type of definite sum at all. A little while ago I was giving a talk about ‘infinity’ that included a look at the simple geometric series
S = ½ + ¼ + ⅛ +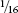 +
+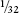 +
+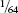 + . . .
+ . . .